
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпlЃКy=x+![]() гыxжсИКАыжсЁЂyжсе§АыжсЗжБ№ЯрНЛгкAЁЂCСНЕуЃЌХзЮяЯпy=Љ
гыxжсИКАыжсЁЂyжсе§АыжсЗжБ№ЯрНЛгкAЁЂCСНЕуЃЌХзЮяЯпy=Љ![]() x2+bx+cОЙ§ЕуBЃЈ1ЃЌ0ЃЉКЭЕуCЃЎ
x2+bx+cОЙ§ЕуBЃЈ1ЃЌ0ЃЉКЭЕуCЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвбжЊЕуQЪЧХзЮяЯпy=Љ![]() x2+bx+cдкЕкЖўЯѓЯоФкЕФвЛИіЖЏЕуЃЎ
x2+bx+cдкЕкЖўЯѓЯоФкЕФвЛИіЖЏЕуЃЎ
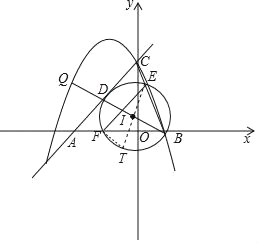
ЂйШчЭМ1ЃЌСЌНгAQЁЂCQЃЌЩшЕуQЕФКсзјБъЮЊtЃЌЁїAQCЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіSЕФзюДѓжЕЃЛ
ЂкСЌНгBQНЛACгкЕуDЃЌСЌНгBCЃЌвдBDЮЊжБОЖзїЁбIЃЌЗжБ№НЛBCЁЂABгкЕуEЁЂFЃЌСЌНгEFЃЌЧѓЯпЖЮEFЕФзюаЁжЕЃЌВЂжБНгаДГіДЫЪБЕуQЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љ![]() x2Љ
x2Љ![]() x+
x+![]() ЃЛЃЈ2ЃЉЂйS=Љ
ЃЛЃЈ2ЃЉЂйS=Љ![]() t2Љ
t2Љ![]() tЃЈЉ3ЃМtЃМ0ЃЉ,
tЃЈЉ3ЃМtЃМ0ЃЉ,![]() ЃЛЂкEF=
ЃЛЂкEF=![]() ЃЌЕуQЕФзјБъЮЊЃЈ
ЃЌЕуQЕФзјБъЮЊЃЈ![]() Љ3ЃЌ4Љ
Љ3ЃЌ4Љ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉИљОнжБЯпЕФНтЮіЪНЕУЕНЕу![]() АбЕуB(1,0)гыЕу
АбЕуB(1,0)гыЕу![]() ДњШы
ДњШы![]() гкЪЧЕУЕННсТлЃЛ
гкЪЧЕУЕННсТлЃЛ
ЃЈ2ЃЉЂйСЌНгOQ,дкжБЯп![]() жа,Сюy=0,дђ
жа,Сюy=0,дђ![]() ЕУЕНЕу
ЕУЕНЕу![]() ИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЕУЕННсТлЃЛ
ИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЕУЕННсТлЃЛ
ЂкНтжБНЧШ§НЧаЮЕУЕН![]() зїжБОЖETНЛЁбIгкЕуT,СЌНгFT,дђ
зїжБОЖETНЛЁбIгкЕуT,СЌНгFT,дђ![]()
ЕУЕН![]() ЕБBDЁЭACЪБЃЌДЫЪБжБОЖBDзюаЁЃЌМДжБОЖETзюаЁЃЌEFЕФжЕзюаЁЃЌЭЦГі
ЕБBDЁЭACЪБЃЌДЫЪБжБОЖBDзюаЁЃЌМДжБОЖETзюаЁЃЌEFЕФжЕзюаЁЃЌЭЦГі![]() дкRtЁїADBжаЃЌИљОнШ§НЧКЏЪ§ЕФЖЈвхМДПЩЕУЕННсТлЃЎ
дкRtЁїADBжаЃЌИљОнШ§НЧКЏЪ§ЕФЖЈвхМДПЩЕУЕННсТлЃЎ
ЪдЬтНтЮіЃК(1)дкжБЯп![]() жа,Сюx=0,дђ
жа,Сюx=0,дђ![]()
ЁрЕу![]()
АбЕуB(1,0)гыЕу![]() ДњШы
ДњШы![]() ЕУЃК
ЕУЃК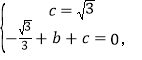
НтЕУЃК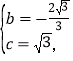
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]()
(2)ЂйСЌНгOQ,дкжБЯп![]() жа,Сюy=0,дђ
жа,Сюy=0,дђ![]()
ЁрЕу![]()
![]()
![]()
![]() МД
МД![]()
ЁрЕБ![]() ЪБ,SзюДѓжЕ
ЪБ,SзюДѓжЕ![]()
ЂкЁпЕуB(1,0), ![]()
![]()
дкRtЁїBOCжа, ![]()
![]()
зїжБОЖETНЛЁбIгкЕуT,СЌНгFT,дђ![]()
гж![]()
ЕБBDЁЭACЪБЃЌДЫЪБжБОЖBDзюаЁЃЌМДжБОЖETзюаЁЃЌEFЕФжЕзюаЁЃЌ
дкRtЁїAOCжа, ![]()
![]()
дкRtЁїADBжаЃЌ![]()
![]()
ДЫЪБЕуQЕФзјБъЮЊ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГНЈжўЙЋЫОМзЁЂввСНИіЙЄГЬЖгЙВЭЌВЮгывЛЯюИФдьЙЄГЬ.вбжЊМзЖгЕЅЖРЭъГЩетЯюЙЄГЬЕФЪБМфЪЧввЖгЕЅЖРЭъГЩетЯюЙЄГЬЪБМфЕФ1.5БЖЃЌгЩгкввЖгЛЙгаЦфЫћШЮЮёЃЌЯШгЩМзЖгЕЅЖРзі45ЬьКѓЃЌдйгЩМзЁЂввСНЖгКЯзі30ЬьЃЌЭъГЩСЫИУЯюИФдьЙЄГЬШЮЮё.
ЃЈ1ЃЉЧѓМзЁЂввСНЖгЕЅЖРЭъГЩИФдьЙЄГЬШЮЮёИїашЖрЩйЬьЃЛ
ЃЈ2ЃЉетЯюИФдьЙЄГЬЙВЭЖзЪ240ЭђдЊЃЌШчЙћАДЭъГЩЕФЙЄГЬСПИЖПюЃЌФЧУДМзЁЂввСНЖгПЩЛёЙЄГЬПюИїЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
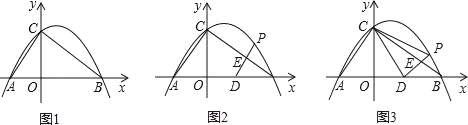
ЁОЬтФПЁПвбжЊЃКRtЁїABCЕФаББпГЄЮЊ5ЃЌаББпЩЯЕФИпЮЊ2ЃЌНЋетИіжБНЧШ§НЧаЮЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЪЙЦфаББпABгыxжсжиКЯЃЈЦфжаOAЃМOBЃЉЃЌжБНЧЖЅЕуCТфдкyжсе§АыжсЩЯЃЈШчЭМ1ЃЉЃЎ
ЃЈ1ЃЉЧѓЯпЖЮOAЁЂOBЕФГЄКЭОЙ§ЕуAЁЂBЁЂCЕФХзЮяЯпЕФЙиЯЕЪНЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕуDЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЕуPЃЈmЃЌnЃЉЪЧИУХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈЦфжаmЃО0ЃЌnЃО0ЃЉЃЌСЌНгDPНЛBCгкЕуEЃЎ
ЂйЕБЁїBDEЪЧЕШбќШ§НЧаЮЪБЃЌжБНгаДГіДЫЪБЕуEЕФзјБъЃЎ
ЂкгжСЌНгCDЁЂCPЃЈШчЭМ3ЃЉЃЌЁїCDPЪЧЗёгазюДѓУцЛ§ЃПШєгаЃЌЧѓГіЁїCDPЕФзюДѓУцЛ§КЭДЫЪБЕуPЕФзјБъЃЛШєУЛгаЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧЯпЖЮ
ЗжБ№ЪЧЯпЖЮ![]() ЁЂ
ЁЂ![]() ЩЯЕФЖЏЕу.
ЩЯЕФЖЏЕу.
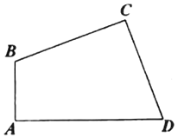
ЃЈ1ЃЉФмЗёдкЯпЖЮ![]() ЩЯзїГіЕуEЃЌдкЯпЖЮ
ЩЯзїГіЕуEЃЌдкЯпЖЮ![]() ЩЯзїГіЕу
ЩЯзїГіЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжмГЄзюаЁЃП______ЃЈгУЁАФмЁБЛђЁАВЛФмЁБЬюПеЃЉЃЛ
ЕФжмГЄзюаЁЃП______ЃЈгУЁАФмЁБЛђЁАВЛФмЁБЬюПеЃЉЃЛ
ЃЈ2ЃЉШчЙћФмЃЌЧыФудкЭМжазїГіТњзуЬѕМўЕФЕу![]() ЁЂ
ЁЂ![]() ЃЈВЛвЊЧѓаДГізїЗЈЃЉЃЌВЂжБНгаДГі
ЃЈВЛвЊЧѓаДГізїЗЈЃЉЃЌВЂжБНгаДГі![]() ЕФЖШЪ§ЃЛШчЙћВЛФмЃЌЧыЫЕУїРэгЩ.
ЕФЖШЪ§ЃЛШчЙћВЛФмЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЕФЖдГЦжсЮЊжБЯп
ЕФЖдГЦжсЮЊжБЯп![]() ЃЌЧвХзЮяЯпгы
ЃЌЧвХзЮяЯпгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌЦфжа
ЕуЃЌЦфжа![]() ЃЌ
ЃЌ![]() .
.

ЃЈ1ЃЉШєжБЯп![]() ОЙ§
ОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧѓжБЯп
СНЕуЃЌЧѓжБЯп![]() КЭХзЮяЯпЕФНтЮіЪНЃЛ
КЭХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжс![]() ЩЯеввЛЕу
ЩЯеввЛЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыгыЕНЕу
ЕФОрРыгыЕНЕу![]() ЕФОрРыжЎКЭзюаЁЃЌЧѓГіЕу
ЕФОрРыжЎКЭзюаЁЃЌЧѓГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕу![]() ЮЊХзЮяЯпЕФЖдГЦжс
ЮЊХзЮяЯпЕФЖдГЦжс![]() ЩЯЕФвЛИіЖЏЕуЃЌЧѓЪЙ
ЩЯЕФвЛИіЖЏЕуЃЌЧѓЪЙ![]() ЮЊжБНЧШ§НЧаЮЕФЕу
ЮЊжБНЧШ§НЧаЮЕФЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЕу
ЃЎЕу![]() ЪЧЩфЯп
ЪЧЩфЯп![]() ЩЯвЛЕуЃЌЕу
ЩЯвЛЕуЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯвЛЕуЃЌЧвЕу
ЩЯвЛЕуЃЌЧвЕу![]() гыЕу
гыЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЃЌСЌНг
ЖдГЦЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌНЛ
ЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЎ
ЃЎ
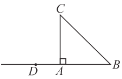
ЃЈ1ЃЉИљОнЬтвтЭъГЩзїЭМЃЛ
ЃЈ2ЃЉЧыФуаДГі![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂНјаажЄУїЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂНјаажЄУїЃЛ
ЃЈ3ЃЉаДГіЯпЖЮ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂНјаажЄУїЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂНјаажЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃдкАЫФъМЖПЊеЙЛЗБЃжЊЪЖЮЪОэЕїВщЛюЖЏЃЌЮЪОэвЛЙВ10ЕРЬтЃЌАЫФъМЖЃЈШ§ЃЉАрЕФЮЪОэЕУЗжЧщПіЭГМЦЭМШчЯТЭМЫљЪОЃК
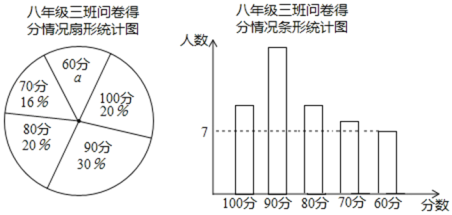
ЃЈ1ЃЉЩШаЮЭГМЦЭМжаЃЌ![]() ______________ЃЛ
______________ЃЛ
ЃЈ2ЃЉИљОнвдЩЯЭГМЦЭМжаЕФаХЯЂЃЌ
ЂйЮЪОэЕУЗжЕФМЋВюЪЧ_____________ЗжЃЛЂкЮЪОэЕУЗжЕФжкЪ§ЪЧ____________ЗжЃЛЂлЮЪОэЕУЗжЕФжаЮЛЪ§ЪЧ______________ЗжЃЛ
ЃЈ3ЃЉЧыФуЧѓГіИУАрЭЌбЇЕФЦНОљЗж.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЧьзЃИФИяПЊЗХ40жмФъЃЌеЙПЊИФИяПЊЗХЕФЛдЛЭГЩОЭЃЌФГжабЇОйАьЪІЩњЪЋДЪДДзїДѓШќЃЌДгВЮШќзїЦЗжабЁГі20ЦЊгХаузїЦЗЃЌдМЦЛЎвЛЕШНБ3ЦЊЃЌЖўЕШНБ5ЦЊЃЌШ§ЕШНБ12ЦЊЃЌКѓОаЃГЄЛсбаОПОіЖЈЃЌдкИУЯюНБРјзмНБН№ВЛБфЕФЧщПіЯТЃЌИїЕШМЖЛёНБЦЊЪ§ЪЕМЪЕїећЮЊЃКвЛЕШНБ4ЦЊЃЌЖўЕШНБ6ЦЊЃЌШ§ЕШНБ10ЦЊЃЌЕїећКѓвЛЕШНБУПЦЊНБН№НЕЕЭ10дЊЃЌЖўЕШНБУПЦЊНБН№НЕЕЭ20дЊЃЌШ§ЕШНБУПЦЊНБН№НЕЕЭ30дЊЃЌЕїећЧАвЛЕШНБН№УПЦЊНБН№БШШ§ЕШНБУПЦЊНБН№Жр320дЊЃЌдђЕїећКѓвЛЕШНБУПЦЊБШЖўЕШНБУПЦЊНБН№Жр___________дЊЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩфЛїЖгЮЊДгМзЁЂввСНУћдЫЖЏдБжабЁАЮвЛШЫВЮМгБШШќЃЌЖдЫћУЧНјааСЫСљДЮВтЪдЃЌВтЪдГЩМЈШчЯТБэЃЈЕЅЮЛЃКЛЗЃЉЃК

ЃЈ1ЃЉЭъГЩБэжаЬюПеЂй ЃЛЂк ЃЛ
ЃЈ2ЃЉЧыМЦЫуМзСљДЮВтЪдГЩМЈЕФЗНВюЃЛ
ЃЈ3ЃЉШєввСљДЮВтЪдГЩМЈЗНВюЮЊ![]() ЃЌФуШЯЮЊЭЦМіЫВЮМгБШШќИќКЯЪЪЃЌЧыЫЕУїРэгЩЃЎ
ЃЌФуШЯЮЊЭЦМіЫВЮМгБШШќИќКЯЪЪЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com