Question

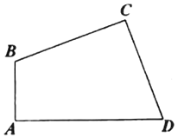
【题目】如图，四边形中，，，、分别是线段、上的动点.

（1）能否在线段上作出点E，在线段上作出点，使的周长最小？______（用“能”或“不能”填空）；

（2）如果能，请你在图中作出满足条件的点、（不要求写出作法），并直接写出的度数；如果不能，请说明理由.

Answer 1

【答案】（1）能；（2）作出满足条件的点、（图见解析），

【解析】

（1）根据对称性能在线段AD上作出点E，在线段DC上作出点F，使△BEF的周长最小；
（2）根据对称性得等腰三角形，再根据三角形内角和即可求出∠EBF的度数．

解：（1）能在线段AD上作出点E，在线段DC上作出点F，使△BEF的周长最小．
故答案为：能．
（2）如图所示：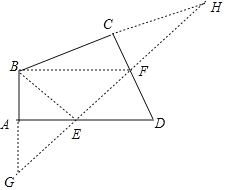

点E、F即为所求作的点．
作点B关于AD和DC的对称点G和H，
连接GH，交AD和DC于点E和F，
连接BE、BF，此时△BEF的周长最小．
由对称性可知：
BF=HF，BE=GE，
∴∠FBH=∠H，∠EBG=∠G，
∵四边形ABCD中，∠D=70°，∠A=∠C=90°，
∴∠ABC=110°，
∴∠H+∠G=70°，
∴∠FBH+∠EBG=70°，
∴∠EBF=110°-70°=40°．