
【题目】已知一元二次方程x2+(1﹣2m)x+m+13=0的两根之积等于两根之和的2倍,则m的值是( )
A. ﹣5 B. 5 C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,∠B=90°,∠A=30°,AC=4,点E在AC上,AE=3.将三角形纸片按图1方式折叠,使点A的对应点![]() 落在AB的延长线上,折痕为ED,
落在AB的延长线上,折痕为ED,![]() 交BC于点F.
交BC于点F.
(1)求∠CFE的度数;
(2)如图2,,继续将纸片沿BF折叠,点![]() 的对应点为
的对应点为![]() ,
,![]() 交DE于点G .求线段DG的长.
交DE于点G .求线段DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE ≌△ACD的是

A.∠B=∠CB.AD=AEC.∠BDC=∠CEBD.BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
时间(天) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
人 数 | 1 | 2 | 4 | 5 | 7 | 11 | 8 | 6 | 4 | 2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
3.5~5.5 | 3 | 0.06 |
5.5~7.5 | 9 | 0.18 |
7.5~9.5 | 0.36 | |
9.5~11.5 | 14 | |
11.5~13.5 | 6 | 0.12 |
合 计 | 50 | 1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑公司甲、乙两个工程队共同参与一项改造工程.已知甲队单独完成这项工程的时间是乙队单独完成这项工程时间的1.5倍,由于乙队还有其他任务,先由甲队单独做45天后,再由甲、乙两队合做30天,完成了该项改造工程任务.
(1)求甲、乙两队单独完成改造工程任务各需多少天;
(2)这项改造工程共投资240万元,如果按完成的工程量付款,那么甲、乙两队可获工程款各多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是( )
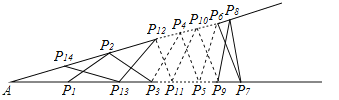
A.14B.13C.12D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 上的动点.
上的动点.
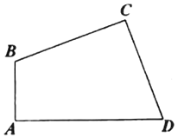
(1)能否在线段![]() 上作出点E,在线段
上作出点E,在线段![]() 上作出点
上作出点![]() ,使
,使![]() 的周长最小?______(用“能”或“不能”填空);
的周长最小?______(用“能”或“不能”填空);
(2)如果能,请你在图中作出满足条件的点![]() 、
、![]() (不要求写出作法),并直接写出
(不要求写出作法),并直接写出![]() 的度数;如果不能,请说明理由.
的度数;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com