
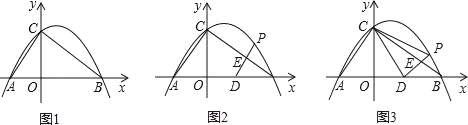
【题目】已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1).
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式.
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标.
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
【答案】(1)![]() (2)①(3,
(2)①(3,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() )②当m=
)②当m=![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为(![]() ,
,![]() ),S△CDP的最大值是
),S△CDP的最大值是![]()
【解析】试题(1)由Rt△ABC中,CO⊥AB可证△AOC∽△COB,由相似比得OC2=OAOB,设OA的长为x,则OB=5-x,代入可求OA,OB的长,确定A,B,C三点坐标,求抛物线解析式;
(2)根据△BDE为等腰三角形,分为DE=EB,EB=BD,DE=BD三种情况,分别求E点坐标;
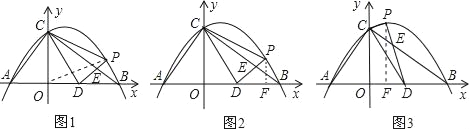
(3)作辅助线,将求△CDP的面积问题转化.方法一:如图1,连接OP,根据S△CDP=S四边形CODP-S△COD=S△COP+S△ODP-S△COD,表示△CDP的面积;方法二:过点P作PE⊥x轴于点F,则S△CDP=S梯形COFP-S△COD-S△DFP,表示△CDP的面积;再利用二次函数的性质求出△CDP的最大面积和此时点P的坐标.
试题解析:
(1)设OA的长为x,则OB=5﹣x;
∵OC=2,AB=5,∠BOC=∠AOC=90°,∠OAC=∠OCB;
∴△AOC∽△COB,∴OC2=OAOB
∴22=x(5﹣x)
解得:x1=1,x2=4,
∵OA<OB,∴OA=1,OB=4;
∴点A、B、C的坐标分别是:A(﹣1,0),B(4,0),C(0,2);
方法一:设经过点A、B、C的抛物线的关系式为:y=ax2+bx+2,
将A、B、C三点的坐标代入得
 …
…
解得:a=![]() ,
,
所以这个二次函数的表达式为:y=![]()
方法二:设过点A、B、C的抛物线的关系式为:y=a(x+1)(x﹣4)…
将C点的坐标代入得:a=-![]()
所以这个二次函数的表达式为:y=![]()
(2)①当△BDE是等腰三角形时,点E的坐标分别是:(3,![]() ),(
),(![]() ,(4-
,(4-![]() ) .
) .
②如图1,连接OP,
S△CDP=S四边形CODP﹣S△COD=S△COP+S△ODP﹣S△COD
=![]()
img src="http://thumb.zyjl.cn/Upload/2019/04/15/10/a0e4069c/SYS201904151009117939279132_DA/SYS201904151009117939279132_DA.016.png" width="218" height="37" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
∴当m=![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为(![]() ,
,![]() ),
),
S△CDP的最大值是![]() .
.
另解:如图2、图3,过点P作PF⊥x轴于点F,则
S△CDP=S梯形COFP﹣S△COD﹣S△DFP
=
∴当m=![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为(![]() ,
,![]() ),
),
S△CDP的最大值是![]() .
.


科目:初中数学 来源: 题型:
【题目】已知OP平分∠AOB,点Q在OP上,点M在OA上,且点Q,M均不与点O重合.在OB上确定点N,使QN =QM,则满足条件的点N的个数为( )
A.1 个B.2个C.1或2个D.无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
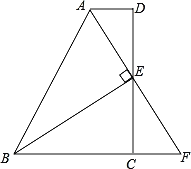
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
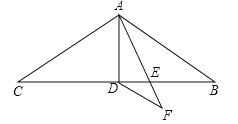
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于检修部分生产设备,生产能力下降,某工厂现在比原计划平均每天少生产30台机器,现在生产600台机器所需时间与原计划生产900台机器所需时间相同.
问现在平均每天生产多少台机器.
(1)设现在平均每天生产![]() 台机器,则用含
台机器,则用含![]() 的式子表示;
的式子表示;
原计划平均每天生产______台机器,现在生产600台机器所需时间为______天,原计划生产900台机器所需时间为______天;
(2)列出方程,完成本题解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=x+![]() 与x轴负半轴、y轴正半轴分别相交于A、C两点,抛物线y=﹣
与x轴负半轴、y轴正半轴分别相交于A、C两点,抛物线y=﹣![]() x2+bx+c经过点B(1,0)和点C.
x2+bx+c经过点B(1,0)和点C.

(1)求抛物线的解析式;
(2)已知点Q是抛物线y=﹣![]() x2+bx+c在第二象限内的一个动点.
x2+bx+c在第二象限内的一个动点.
①如图1,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 ,x2 ,且x12+x22=10,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com