
| x | … | 1 | 2 | 3 | 4 | 5 | … |
| m | … | 1.5 | 1.4 | 1.3 | 1.2 | 1.1 | … |
分析 (1)由表格数据可知甲种水果每吨的销售利润m(万元)与销售量x(吨)之间的函数关系式是一次函数,利用待定系数法求得答案即可;
(2)表示出乙种水果的销售利润与甲种水果的销售利润建立方程求得答案即可;
(3)设销售甲种水果x吨,则销售乙种水果16-x吨,求得销售利润之和,利用函数的性质求得最大利润即可.
解答 解:(1)设甲种水果每吨的销售利润m(万元)与销售量x(吨)之间的函数关系式m=kx+b,
把(1,1.5),(2,1.4)代入得$\left\{\begin{array}{l}{k+b=1.5}\\{2k+b=1.4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-0.1}\\{b=1.6}\end{array}\right.$.
∴m=-0.1x+1.6,
∴甲种水果的销售利润y=mx=(-0.1x+1.6)x=-0.1x2+1.6x,
因此甲种水果的销售利润y(万元)与销售量x(吨)之间的函数关系式y=-0.1x2+1.6x;
(2)乙种水果的销售利润y=0.4x,
由题意得0.4x=-0.1x2+1.6x
解得:x=12或0(舍去),
所以两种水果的销售量与销售利润能同时相等,此时甲种水果的销售量为12吨;
(3)设销售甲种水果x吨,则销售乙种水果16-x吨,由题意得
总销售利润y=-0.1x2+1.6x+0.4(16-x)=-0.1x2+1.2x+6.4,(0≤x≤16)
∵a=-0.1<0,
∴抛物线开口向下,
∵x=-$\frac{b}{2a}$=$\frac{1.2}{2×0.1}$=6,
∴当x=6时,ymax=-0.1×36+1.2×6+6.4=10(万元),
∴当x=6时,函数最大值是10,
即销售甲种水果6吨,销售乙种水果10吨,销售利润最大为10万元.
点评 此题考查一次函数的实际运用,待定系数法求函数解析式,掌握待定系数法求函数解析式以及函数的性质是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
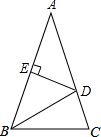 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AB于点E,交AC于点D,△ABC,△DBC的周长分别是60和38,求AC,BC的长.
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AB于点E,交AC于点D,△ABC,△DBC的周长分别是60和38,求AC,BC的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com