
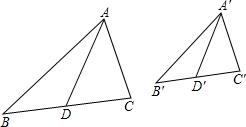
 如图,△ABC∽△A′B′C′,AD、A′D′分别是它们的中线,求证:AD:A′D′=AB:A′B′.
如图,△ABC∽△A′B′C′,AD、A′D′分别是它们的中线,求证:AD:A′D′=AB:A′B′. 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
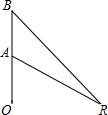 如图,一枚运载火箭从地面O处发射,当火箭到达点A处时,地面R处的雷达站测得AR的距离是6km,仰角为30°.5s后,火箭到达点B处,此时BR的距离为6.25km,仰角为45°.求火箭从A处到B处的平均速度(结果精确到1m/s)
如图,一枚运载火箭从地面O处发射,当火箭到达点A处时,地面R处的雷达站测得AR的距离是6km,仰角为30°.5s后,火箭到达点B处,此时BR的距离为6.25km,仰角为45°.求火箭从A处到B处的平均速度(结果精确到1m/s)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com