
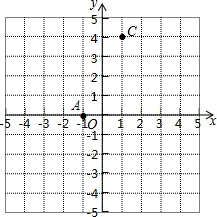
 如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.分析 (1)分点B在点A的左边和右边两种情况解答;
(2)利用三角形的面积公式列式计算即可得解;
(3)利用三角形的面积公式列式求出点P到x轴的距离,然后分两种情况写出点P的坐标即可.
解答 解:(1)点B在点A的右边时,-1+3=2,
点B在点A的左边时,-1-3=-4,
所以,B的坐标为(2,0)或(-4,0),
如图所示: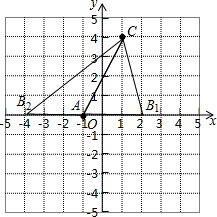
(2)△ABC的面积=$\frac{1}{2}$×3×4=6;
(3)设点P到x轴的距离为h,
则$\frac{1}{2}$×3h=10,
解得h=$\frac{20}{3}$,
点P在y轴正半轴时,P(0,$\frac{20}{3}$),
点P在y轴负半轴时,P(0,-$\frac{20}{3}$),
综上所述,点P的坐标为(0,$\frac{20}{3}$)或(0,-$\frac{20}{3}$).
点评 本题考查了坐标与图形性质,主要利用了三角形的面积,难点在于要分情况讨论.


科目:初中数学 来源: 题型:解答题
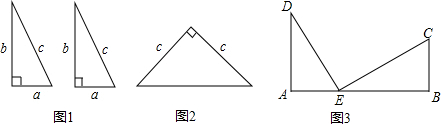
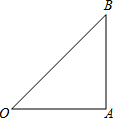 如图,Rt△ABC中,∠OAB=90°,OA=AB=2,
如图,Rt△ABC中,∠OAB=90°,OA=AB=2,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
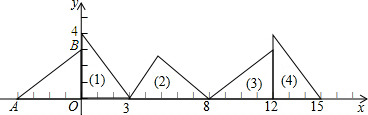
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
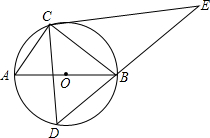 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | 5 | B. | 8 | C. | $\frac{32}{5}$ | D. | $\frac{20}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
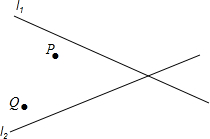 如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).
如图,邳州电讯公司要修建一座信号发射塔,按设计要求,发射塔到两城镇P、Q的距离相等,并且到两条公路l1、l2的距离也相等,请你帮助设计员在图中画出发射塔的位置(使用尺规作图,保留作图痕迹).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com