
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
(1)求抛物线y=ax2+bx+2的函数表达式;
(2)若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.
【答案】
(1)
解:把点A(﹣2,0),B(2,2)代入抛物线y=ax2+bx+2中,
![]() ,
,
解得: 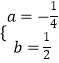 ,
,
∴抛物线函数表达式为:y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:y=﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ;
;
∴对称轴是:直线x=1,
如图1,过B作BE⊥x轴于E,
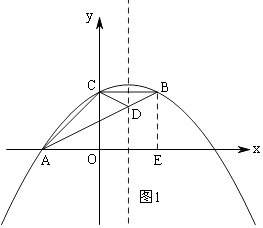
∵C(0,2),B(2,2),对称轴是:x=1,
∴C与B关于x=1对称,
∴CD=BD,
连接AB交对称轴于点D,此时△ACD的周长最小,
∵BE=2,AE=2+2=4,OC=2,OA=2,
∴AB= ![]() =2
=2 ![]() ,
,
AC= ![]() =2
=2 ![]() ,
,
∴△ACD的周长=AC+CD+AD=AC+BD+AD=AC+AB=2 ![]() +2
+2 ![]() ;
;
答:△ACD的周长的最小值是2 ![]() +2
+2 ![]()
(3)
解:存在,
分两种情况:
①当∠ACP=90°时,△ACP是直角三角形,如图2,
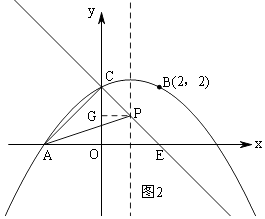
过P作PD⊥y轴于D,
设P(1,y),
则△CGP∽△AOC,
∴ ![]() ,
,
∴ ![]() ,
,
∴CG=1,
∴OG=2﹣1=1,
∴P(1,1);
②当∠CAP=90°时,△ACP是直角三角形,如图3,
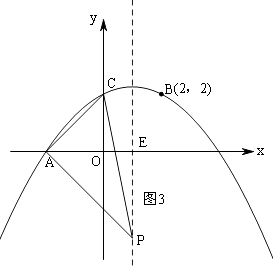
设P(1,y),
则△PEA∽△AOC,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PE=3,
∴P(1,﹣3);
综上所述,△ACP是直角三角形时,点P的坐标为(1,1)或(1,﹣3).
【解析】(1)利用待定系数法求抛物线的函数表达式;(2)由轴对称的最短路径得:因为B与C关于对称轴对称,所以连接AB交对称轴于点D,此时△ACD的周长最小,利用勾股定理求其三边相加即可;(3)存在,当A和C分别为直角顶点时,画出直角三角形,设P(1,y),根据三角形相似列比例式可得P的坐标.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() .
.
(1)求![]() 的面积;
的面积;
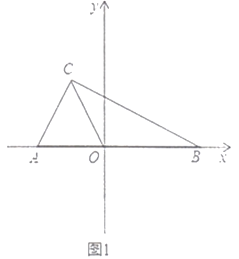
(2)点![]() 为坐标轴上一点,若
为坐标轴上一点,若![]() 的面积恰好是
的面积恰好是![]() 面积的一半,求点
面积的一半,求点![]() 的坐标.
的坐标.
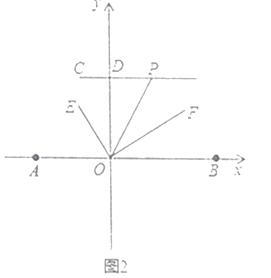
(3)如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 延长线上的一动点,连接
延长线上的一动点,连接![]() 平分
平分![]() .当点
.当点![]() 运动时,
运动时,![]() 与
与![]() 度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
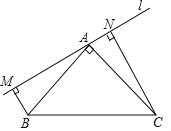
【题目】等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N
(1)你能找到一对三角形的全等吗?并说明理由.
(2)BM,CN,MN之间有何关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°.
(1)尺规作图:作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)的条件下,连接BD,当BC=5cm,AB=13cm时,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论错误的是( )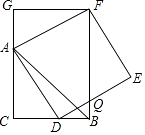
A.AC=FG
B.S△FAB:S四边形CBFG=1:2
C.AD2=FQAC
D.∠ADC=∠ABF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要新建一个800平方米的长方形场地,且其长、宽的比为5:2.
(1)求这个长方形场地的长和宽为多少米?
(2)某个正方形场地的周围有一圈金属栅栏围墙,如果把原来面积为900平方米的正方形场地的栅栏围墙全部利用,来作为新场地的长方形围墙,栅栏围墙是否够用?为什么?(提示:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com