
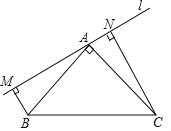
【题目】等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N
(1)你能找到一对三角形的全等吗?并说明理由.
(2)BM,CN,MN之间有何关系?
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】2015年4月份的尼泊尔强震曾经导致珠峰雪崩,在珠峰抢险时,需8组登山队员步行运送物资,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人;若按每组人数比预定人数少分配1人,则总数不够90人,那么预定每组分配的人数是( )
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病,呼吸道疾病等,给人们造成困扰.为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图.

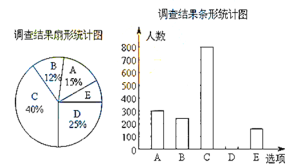
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有_________人;
(2)扇形统计图中,扇形![]() 的圆心角度数是__________;
的圆心角度数是__________;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,过△ABC的顶点B作直线![]() ,且点A到
,且点A到![]() 的距离为2,点C到
的距离为2,点C到![]() 的距离为3,则AC的长是( )
的距离为3,则AC的长是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
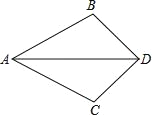
【题目】如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件________;
(2)根据“ASA”需添加条件________;
(3)根据“AAS”需添加条件________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)求证:到线段两端距离相等的点在线段的垂直平分线上.(要求:画出图形,写出已知,求证和证明过程)
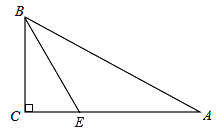
(2)用(1)中的结论解决:如图,△ABC中,∠A=30°,∠C=90°,BE平分∠ABC, 求证:点E在线段AB的垂直平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
(1)求抛物线y=ax2+bx+2的函数表达式;
(2)若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.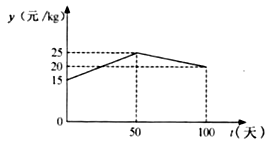
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com