
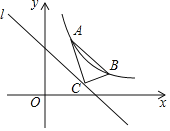
【题目】如图,已知点A(m,m+3),点B(n,n﹣3)是反比例函数y=![]() (k>0)在第一象限的图象上的两点,连接AB.将直线AB向下平移3个单位得到直线l,在直线l上任取一点C,则△ABC的面积为( )
(k>0)在第一象限的图象上的两点,连接AB.将直线AB向下平移3个单位得到直线l,在直线l上任取一点C,则△ABC的面积为( )
A.![]() B.6C.
B.6C.![]() D.9
D.9
【答案】A
【解析】
由点A(m,m+3),点B(n,n﹣3)在反比例函数y=![]() (k>0)第一象限的图象上,可得到m、n之间的关系,过点A、B分别作x轴、y轴的平行线,构造直角三角形,可求出直角三角形的直角边的长,由平移可得直角三角形的直角顶点在直线l上,进而将问题转化为求△ADB的面积.
(k>0)第一象限的图象上,可得到m、n之间的关系,过点A、B分别作x轴、y轴的平行线,构造直角三角形,可求出直角三角形的直角边的长,由平移可得直角三角形的直角顶点在直线l上,进而将问题转化为求△ADB的面积.
解:∵点A(m,m+3),点B(n,n﹣3)在反比例函数y=![]() (k>0)第一象限的图象上,
(k>0)第一象限的图象上,
∴k=m(m+3)=n(n﹣3),
即:(m+n)(m﹣n+3)=0,
∵m+n>0,
∴m﹣n+3=0,即:m﹣n=﹣3,
过点A、B分别作x轴、y轴的平行线相交于点D,
∴BD=xB﹣xA=n﹣m=3,AD=yA﹣yB=m+3﹣(n﹣3)=m﹣n+6=3,
又∵直线l是由直线AB向下平移3个单位得到的,
∴平移后点A与点D重合,
因此,点D在直线l上,
∴S△ACB=S△ADB=![]() ADBD=
ADBD=![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”译文:“今有甲乙二人,不知其钱包里有多少钱.若乙把自己一半的钱给甲,则甲的钱数为50钱;而甲把自己![]() 的钱给乙,则乙的钱数也为50钱.问甲、乙各有多少钱?”设甲、乙原有钱数分别为
的钱给乙,则乙的钱数也为50钱.问甲、乙各有多少钱?”设甲、乙原有钱数分别为![]() 、
、![]() ,下列所列方程组正确的是( )
,下列所列方程组正确的是( )
A.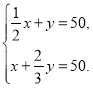 B.
B.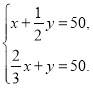 C.
C.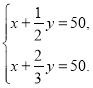 D.
D.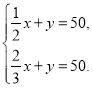
查看答案和解析>>
科目:初中数学 来源: 题型:
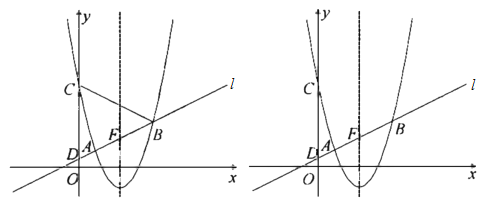
【题目】如图,在平面直角坐标系![]() 中,以直线
中,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)设直线![]() 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为![]() ,
,![]() 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若![]() ,且
,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
(3)若在![]() 轴上有且只有一点
轴上有且只有一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 依次是边
依次是边![]() 的四等分点,点
的四等分点,点![]() ,
,![]() ,
,![]() 依次是边
依次是边![]() 的四等分点,分别以
的四等分点,分别以![]() ,
,![]() ,
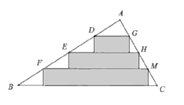
,![]() 为边向下剪三个宽相等的矩形,如图所示.若图中空白部分的面积和为
为边向下剪三个宽相等的矩形,如图所示.若图中空白部分的面积和为![]() ,则图中阴影部分的面积和是( )
,则图中阴影部分的面积和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚![]() 处测得一座建筑物顶点
处测得一座建筑物顶点![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处再测得该建筑物顶点
处再测得该建筑物顶点![]() 的仰角为
的仰角为![]() .已知
.已知![]() 米,
米,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,山坡坡度为
,山坡坡度为![]() (即
(即![]() ).注:取
).注:取![]() 为
为![]() .
.
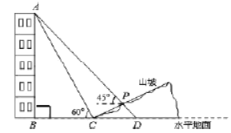
(1)求该建筑物的高度(即![]() 的长).
的长).
(2)求此人所在位置点![]() 的铅直高度(测倾器的高度忽略不计).
的铅直高度(测倾器的高度忽略不计).
(3)若某一时刻,![]() 米长木棒竖放时,在太阳光线下的水平影长是
米长木棒竖放时,在太阳光线下的水平影长是![]() 米,则同一时刻该座建筑物顶点
米,则同一时刻该座建筑物顶点![]() 投影与山坡上点
投影与山坡上点![]() 重合,求点
重合,求点![]() 到该座建筑物的水平距离.
到该座建筑物的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2﹣2x﹣3,一次函数y2=x﹣1.
(1)在同一坐标系中,画出这两个函数的图象;
(2)根据图形,求满足y1>y2的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③对于任意实数m,a+b≥am2+bm总成立;
④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com