
【题目】1952个正整数1,2,3,4,…,1952按如图方式排列成一个表:
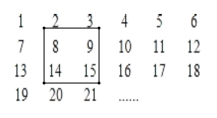
(1)如图,用一正方形方框任意框住4个数,记左上角的一个数为x,当被框住的4个数之和等于358时,x的值为多少?
(2)如(1)中方式,能否框住这样的4个数,它们的和等于2438?若能,则求出x的值;若不能,则说明理由.
(3)从左到右,第1到第6列各列数之和分别记为a1,a2,a3,a4,a5,a6,则这6个数中,最大数与最小数之差等于 .(直接填出结果,不写计算过程)
【答案】(1)86;(2)不能,理由见解析;(3)1627.
【解析】
(1)由正方形框可知,每行以6为循环,所以横向相邻两个数之间相差1,竖向两个数之间相差6,用含x的式子表示出框住的四个数,根据题意得到关于x的方程,解方程即可得;
(2)用含x的式子表示出框住的四个数,根据题意得到关于x的方程,解方程后进行判断即可;
(3)先确定出1952在哪一行哪一列,根据题意可知如果数字正好排成n行6列,则后面一列的数之和比前一列数之和大n ,据此确定出哪列数之和最大,哪列数之和最小即可求得答案.
(1)记左上角的一个数为x,则另外三个数用含x的式子表示出来,从小到大依次是x+1,x+6,x+7,
则x+(x+1)+(x+6)+(x+7)=358,
解得:x=86,
答:x的值为86;
(2)不能,理由如下:
∵x+(x+1)+(x+6)+(x+7)=2438时,
x=606,左上角的数不能是6的倍数,
∴它们的和不能等于2438;
(3)1952÷6=325…2,
∴1952在第326行第2列,
∴排到1950时,共排了325行,6列,后面的每一列数之和都比前一列数之和大325,
第6列比第1列大325×5=1625,
排到1952时,此时第1列、第2列有数字326个,其余各列仍然是325个数字,
此时第1列数之和比第6列数之和大1951-1625=326,
第2列数之和比第1列数之和大326,
∴a2最大,a3最小,
∴最大数与最小数之差=1952-325=1627,
故答案为:1627.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________
的坐标为__________
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形.
是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
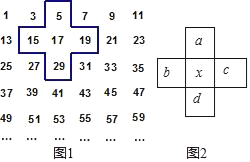
【题目】如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若x=17,则a+b+c+d= .
(2)移动十字框,用x表示a+b+c+d= .
(3)设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
-3,9,-27,81,…;①
1,-3,9,-27,…;②
-1,11,-25,83,…;③
(1)第①行数按什么规律排列?第10个数是________;
(2)第②③行数与第①行数分别有什么关系?
(3)设x、y、z分别为第①②③行的第2018个数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荔枝上市后,某水果店的老板用500元购进第一批荔枝,销售完后,又用800元购进第二批荔枝,所购件数是第一批购进件数的2倍,但每件进价比第一批进价少5元.
(1)求第一批荔枝每件的进价;
(2)若第二批荔枝以30元/件的价格销售,在售出所购件数的![]() 后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元?
后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
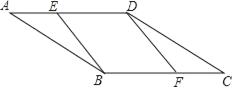
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )
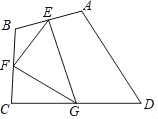
A. 8 B. 12 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
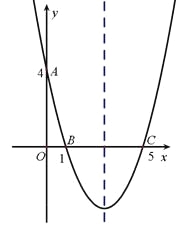
(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,a、c满足![]() .AB表示点A、B之间的距离,且
.AB表示点A、B之间的距离,且![]() .
.
![]()
(1)![]() ________,
________,![]() ________;
________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数________表示的点重合;
(3)点A、B、C在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则![]() ________,
________,![]() ________.(用含t的代数式表示)
________.(用含t的代数式表示)
(4)在(3)的条件下,请问:![]() 的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com