
【题目】如图1,在平面直角坐标系中,![]() ,
,![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,若
,若![]() 与
与![]() 互为相反数.
互为相反数.


(1)求![]() 的值;
的值;
(2)如图2,![]() 交
交![]() 轴于
轴于![]() ,以
,以![]() 为边的正方形
为边的正方形![]() 的对角线
的对角线![]() 交
交![]() 轴于
轴于![]() .
.
①求证:![]() ;
;
②记![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①见解析,②3
;(2)①见解析,②3
【解析】
(1)根据相反数的概念得出方程![]() ,求出
,求出![]() 的值,作AG⊥OB于G,利用含30度角的直角三角形的性质即可求得答案;
的值,作AG⊥OB于G,利用含30度角的直角三角形的性质即可求得答案;
(2)①延长AC交y轴于点Q,作AP⊥OA交OB于P,利用“ASA”证得△OAQ![]() △PAB,得到AQ= AB,
△PAB,得到AQ= AB,![]() ,QC=2OC,再利用线段的和差即可证明;
,QC=2OC,再利用线段的和差即可证明;
②连接QF,利用“SAS”证得△FAQ![]() △FAB,得到
△FAB,得到![]() ,从而证得结论.
,从而证得结论.
(1)∵![]() 和
和![]() 互为相反数,
互为相反数,
∴![]() ,
,
∴![]() ,
,![]()
![]() ,
,
∴![]() ,
,
如图:作AG⊥OB于G,
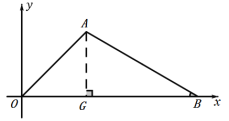
∵点A的坐标为(![]() ,
,![]() ),即A (
),即A (![]() ,
,![]() ),
),
∴AG=OG=2,
在Rt![]() BAG中,∠ABG=30
BAG中,∠ABG=30![]() ,AG=2,
,AG=2,
∴AB=2AG=4,
BG=![]() ,
,
∴BO= OG+ BG=2+![]() ,
,
∴![]() ;
;
(2)①延长AC交![]() 轴于点Q,作AP⊥OA交OB于P,如图:
轴于点Q,作AP⊥OA交OB于P,如图:
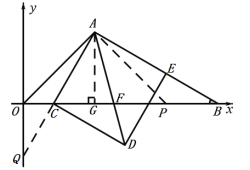
由(1)得AG=OG=2,AG⊥OB,
∴∠AOG=45![]() ,
,
∵AP⊥OA,
∴∠APO=90![]() -∠AOG =45
-∠AOG =45![]() ,
,
∴∠APO=∠AOG=45![]() ,
,
∴AO=AP,∠APB=180![]() -45
-45![]() =135
=135![]() ,
,
∠AOQ=90![]() +45
+45![]() =135
=135![]() ,
,
∴∠APB=∠AOQ,
∵AP⊥OA,AC⊥AB,
∴∠OAP=∠CAB=90![]() ,
,
∴∠OAQ+∠CAP =∠PAB+∠CAP =90![]() ,
,
∴∠OAQ=∠PAB,
在△OAQ和△PAB中,
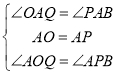 ,
,
∴△OAQ![]() △PAB(ASA),
△PAB(ASA),
∴AQ= AB,![]() ,
,
在Rt![]() OQC中,∠OQC=30
OQC中,∠OQC=30![]() ,
,
∴QC=2OC,
∵四边形ACDE为正方形,
∴AC=AE,
∴BE=AB-AE=AQ-AC=QC=2OC;
②如图,连接QF,
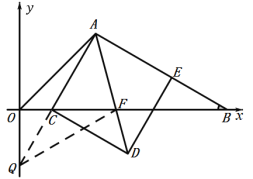
∵四边形ACDE为正方形,AD为对角线,
∴![]() ,
,
由①得:AQ= AB,![]() ,QC=2OC,
,QC=2OC,
∴![]() ,
,
在△FAQ和△FAB中,
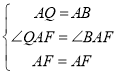 ,
,
∴△FAQ![]() △FAB (SAS),
△FAB (SAS),
∴QF=BF,
∴![]() ,
,
∴![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积;
(2)若连接AD、CF,则这两条线段之间的关系是________________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为1的圆从原点沿数轴向左滚动一周,圆上与原点重合的点O到达O′,设点O′表示的数为a.
(1)求a的值;
(2)求﹣(a﹣![]() )﹣π的算术平方根.
)﹣π的算术平方根.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中 ![]() ,
, ![]() ,斜边AB=6cm,DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O,与D1E1相交于点F .
,斜边AB=6cm,DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O,与D1E1相交于点F . 
(1)求 ![]() 的度数;
的度数;
(2)求线段AD1的长;
(3)若把三角形D1CE1绕着点 C 顺时针再旋转30°得△D2CE2 , 这时点B在△D2CE2的内部、外部、还是边上?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,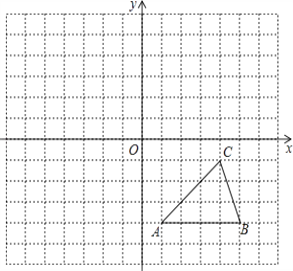
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1 , 画出△A1B1C1 .
(3)求(2)中C到C1经过的路径以及OB扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有一个长方形ABCD,AB=4,BC=3且AB∥x轴,BC∥y轴,把这个长方形首先向左平移7个单位,再向上平移5个单位,然后沿着y轴翻折得长方形A1B1C1D1,在这个过程中A与A1,B与B1,C与C1,D与D1分别表示始末位置长方形中相同位置的顶点,已知A1坐标是(5,1),那么A点坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.甲同学的作法如图1所示,乙同学的作法如图2所示,对于两人的作法,下列说法正确的是( )
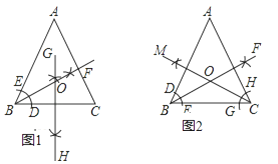
A.两人都对B.两人都不对C.甲对,乙不对D.乙对,甲不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com