
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=4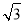 .将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= 度;
(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.

(1) 15°;(2)  ;(3) 当0≤x≤2时,y=?
;(3) 当0≤x≤2时,y=?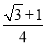 x2+4x+8;当2<x≤6-2
x2+4x+8;当2<x≤6-2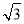 时,y=?
时,y=?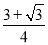 x2+18;当6-2
x2+18;当6-2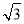 <x≤6时,y=
<x≤6时,y= x2-6
x2-6 x+18
x+18 .
.
【解析】
试题分析:(1)如题图2所示,由三角形的外角性质可得;
(2)如题图3所示,在Rt△ACF中,解直角三角形即可;
(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况:
(I)当0≤x≤2时,如图1所示;
(II)当2<x≤6-2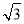 时,如图2所示;
时,如图2所示;
(III)当6-2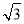 <x≤6时,如图3所示.
<x≤6时,如图3所示.
试题解析:(1)如题图2所示,
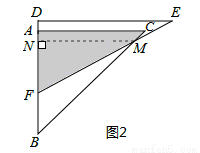
∵在三角板DEF中,∠FDE=90°,DF=4,DE=4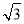 ,
,
∴tan∠DFE=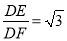 ,
,
∴∠DFE=60°,
∴∠EMC=∠FMB=∠DFE-∠ABC=60°-45°=15°;
(2)如题图3所示,当EF经过点C时,

FC= ;
;
(3)在三角板DEF运动过程中,
(I)当0≤x≤2时,如答图1所示:
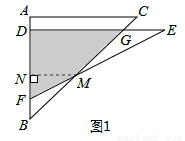
设DE交BC于点G.
过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF= ,BN=NF+BF,
,BN=NF+BF,
∴NF+BF=MN,即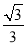 MN+x=MN,解得:MN=
MN+x=MN,解得:MN=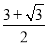 x.
x.
y=S△BDG-S△BFM=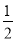 BD•DG-
BD•DG-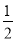 BF•MN=
BF•MN=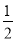 (x+4)2-
(x+4)2-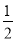 x×
x×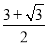 x
x
=?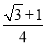 x2+4x+8;
x2+4x+8;
(II)当2<x≤6-2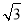 时,如图2所示:
时,如图2所示:

过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF= ,BN=NF+BF,
,BN=NF+BF,
∴NF+BF=MN,即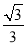 MN+x=MN,解得:MN=
MN+x=MN,解得:MN=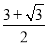 x.
x.
y=S△ABC-S△BFM=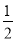 AB•AC-
AB•AC-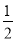 BF•MN=
BF•MN=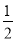 ×62-
×62-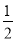 x×
x×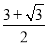 x.
x.
=?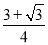 x2+18;
x2+18;
当6-2 <x≤6时,如图3所示:
<x≤6时,如图3所示:
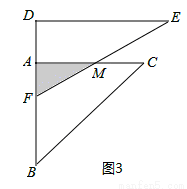
由BF=x,则AF=AB-BF=6-x,
设AC与EF交于点M,则AM=AF•tan60°= (6-x).
(6-x).
y=S△AFM=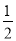 AF•AM=
AF•AM=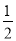 (6-x)×
(6-x)× (6-x)
(6-x)
= x2-6
x2-6 x+18
x+18 .
.
考点:相似形综合题.


科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:解答题
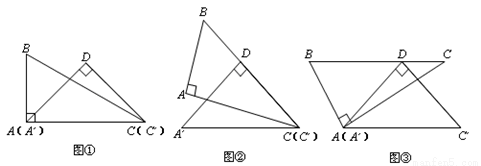
现有一副直角三角板,已知含45°角的直角三角板的斜边恰与含30°角的直角三角板的较长直角边完全重合(如图①).即△C?DA?的顶点A?、C?分别与△BAC的顶点A、C重合.现在让△C?DA?固定不动,将△BAC通过变换使斜边BC经过△C?DA?的直角顶点D.
(1)如图②,将△BAC绕点C按顺时针方向旋转角度α(0°<α<180°),使BC边经过点D,则α= °
(2)如图③,将△BAC绕点A按逆时针方向旋转,使BC边经过点D.试说明:BC∥A?C?.
(3)如图④,若将△BAC沿射线A?C?方向平移m个单位长度,使BC边经过点D,已知AB= ,求m的值.
,求m的值.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省苏州市高新区中考学二模数试卷(解析版) 题型:解答题
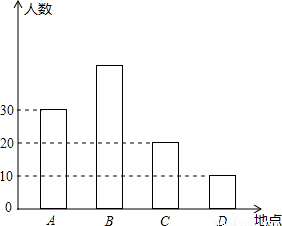
如图,暑假快要到了,某市准备组织同学们分别到A,B,C,D四个地方进行夏令营活动,前往四个地方的人数.
(1)去B地参加夏令营活动人数占总人数的40%,根据统计图求去B地的人数?
(2)若一对姐弟中只能有一人参加夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.用列表法或树形图分析这种方法对姐弟俩是否公平?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省苏州市高新区中考学二模数试卷(解析版) 题型:填空题
如果圆锥的底面圆的半径是8,母线的长是15,那么这个圆锥侧面展开图的扇形的圆心角的度数是 度。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省盐城市亭湖区中考一模数学试卷(解析版) 题型:解答题
如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1.
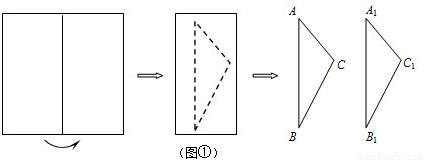
(1)将△ABC,△A1B1C1如图②摆放,使点A1与B重合,点B1在AC边的延长线上,连接CC1交BB1于点E.
①求证:四边形C1B1AB为梯形.
②若∠A=45°, ∠ABC=30°, 求∠B1C1C的度数
(2)若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
(3)在(2)的条件下,若AC=3,B1C1=6,设A1B=x,C1F=y,写出y与x的函数关系式(不要求写出自变量的取值范围)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省淮安市洪泽县九年级中考二模数学试卷(解析版) 题型:填空题
妈妈给小明买笔记本和圆珠笔.已知每本笔记本4元,每支圆珠笔3元,妈妈买了m本笔记本,n支圆珠笔.妈妈共花费 元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com