
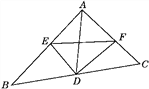
【题目】如图,△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE,DF分别交AB,AC于E,F,且BE2+CF2=EF2,求证:△ABC为直角三角形.
【答案】见解析
【解析】试题分析:延长FD到点M,使DM=DF,连接BM,可证得△CDF≌△BDM,根据全等三角形的性质可得∠DBM=∠C,BM=CF,由∠EDF=90°,MD=FD,根据线段垂直平分线的性质可得EM=EF;再由BE2+CF2=EF2,可得BE2+BM2=EM2,根据勾股定理的逆定理可得△BEM为直角三角形,再证得BM∥AC,由平行线的性质即可证得∠BAC=90°,结论得证.
试题解析:
证明:延长FD至M,使MD=FD,连接MB,ME,如图所示,
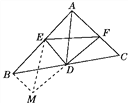
∵D为BC的中点,∴BD=DC,又MD=FD,∠BDM=∠CDF,
∴△BDM≌△CDF(SAS),∴∠DBM=∠C,BM=CF,
∵∠EDF=90°,MD=FD,∴EM=EF,
∵BE2+CF2=EF2,∴BE2+BM2=EM2,
即△BEM为直角三角形,且∠EBM=90°.
由∠DBM=∠C知,BM∥AC,∴∠BAC=180°-∠EBM=90°,
即△ABC为直角三角形.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】一元二次方程x2﹣4x﹣12=0的两根分别是一次函数y=kx+b在x轴上的横坐标和y轴上的纵坐标,则这个一次函数图象与两坐标轴所围成的三角形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查八年级部分女生;
方案二:调查八年级部分男生;
方案三:到八年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整; 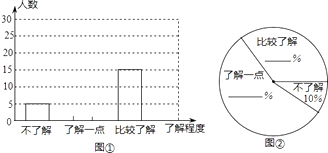
(3)请你估计该校八年级约有多少名学生比较了解“低碳”知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(﹣1)2012+(π﹣3.14)0﹣(﹣ ![]() )﹣1
)﹣1
(2)化简求值:(2x+y)2﹣(2x﹣y)(x+y)﹣2(x﹣2y)(x+2y),其中x= ![]() ,y=﹣2.
,y=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量![]() (件)与时间
(件)与时间![]() (时)的函数图象如图所示.
(时)的函数图象如图所示.

(1)求甲组加工零件的数量y与时间![]() 之间的函数关系式.
之间的函数关系式.
(2)求乙组加工零件总量![]() 的值.
的值.
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
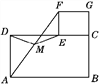 ①
① ②
②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com