
����Ŀ���ڡ�ABC�У�AB��AC����BAC��90�㣬��DΪAC��һ���㣮
��1����ͼ1����E����F��������BD�ϵĵ㲢������AE��AF����EAF��90�㣮��֤����ABE�ա�ACF��
��2���ڣ�1���������£���֤��CF��BD��
��3���ɣ�1������֪����AFB��45�㣬��ͼ2������D��λ�÷����仯ʱ������C��CF��BD��F������AF����ô��AFB�Ķ����Ƿ����仯����֤����Ľ��ۣ�

���𰸡���1�������������2�������������3����AFB��45�㲻�仯�������������.
��������
��1���á�BAE����CAF������֪AB��AC��AE��AF���ɵ���ABE�ա�ACF��
��2��������á�ABE+��BDA��90�㣬����1���á�ABE����ACF������BDA����CDF���ɵô���
(3) ��AFB��45�㲻�仯���������£�����A��AF�Ĵ��߽�BM�ڵ�E����֤����ABE�ա�ACF���ɵ�AE��AF����AEF�ǵ���ֱ������������AFB��45����
��1���ߡ�BAC����BAE+��EAD��90�㣬��EAF����CAF+��EAD��90��
���BAE����CAF
�ڡ�ABE�͡�ACF��

���ABE�ա�ACF��SAS��
��2���ߡ�BAC��90��
���ABE+��BDA��90�㣬
�ɣ�1���á�ABE�ա�ACF
���ABE����ACF
���BDA+��ACF��90��
�֡ߡ�BDA����CDF
���CDF+��ACF��90��
���BFC��90��
��CF��BD
��3����AFB��45�㲻�仯���������£�
����A��AF�Ĵ��߽�BM�ڵ�E

��CF��BD
���BAC��90��
���ABD+��BDA��90��
ͬ����ACF+��CDF��90��
�ߡ�CDF����ADB
���ABD����ACF
ͬ��1�����á�BAE����CAF
�ڡ�ABE�͡�ACF��

���ABE�ա�ACF��ASA��
��AE��AF
���AEF�ǵ���ֱ��������
���AFB��45�㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶��2��ֱ��l���O�ཻ��A��B���㣬M��N�ǡ�O�ϵ��������㣬����ֱ��l����࣬����AMB=45�㣬���ı���MANB��������ֵ�ǣ� �� 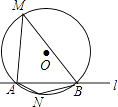
A.2 ![]()
B.4
C.4 ![]()
D.8 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ�ְ�װ�еı���չ��ͼ������Χ�����ɵõ�һ���������ģ�ͣ�
��1�����������ģ�͵�������
��2����ͼ2�Ǹ���a��b��h��ȡֵ�����ļ����������ͼ����ͼ��ͼ��ʵ�߱�ʾ�ij����Σ������������л����ü����������ͼ��
��3����h=a+b����a��b���� ![]() a2+b2��a��6b+10=0����ü�����ı������
a2+b2��a��6b+10=0����ü�����ı������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABC�У���BAC=90�㣬��D��BC���ϣ���BD=BA������B��AD�Ĵ��߽�AC�ڵ�O����OΪԲ�ģ�AOΪ�뾶��Բ��
��1����֤��BC�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ8��tan��C= ![]() �����߶�AB�ij���sin��ADB��ֵ��
�����߶�AB�ij���sin��ADB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��y�Ķ�Ԫһ�η�����![]() �ĽⶼΪ������
�ĽⶼΪ������
��1����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����������Ԫһ�η�����Ľ���һ�����������ε�һ������һ���ױߵij�����������������ε��ܳ�Ϊ9����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�������������⣬�ٰ�Ҫ�����������⣺
���⣺�����ʽy2+4y+8����Сֵ��
�⣺y2+4y+8=y2+4y+4+4=��y+2��2+4
����y+2��2��0
����y+2��2+4��4
��y2+4y+8����Сֵ��4��
��1�������ʽm2+m+4����Сֵ��
��2�������ʽ4��x2+2x�����ֵ��
��3��ij����С��Ҫ��һ��һ�߿�ǽ��ǽ��15m���Ŀյ��Ͻ�һ�������λ�ABCD����һ�߿�ǽ�����������ܳ�Ϊ20m��դ��Χ�ɣ���ͼ����AB=x��m�������ʣ���xȡ��ֵʱ�������������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��OAB�Ķ���A��B������ֱ���A��0��5����B��3��1��������B��BC��AB��ֱ��y=��m��m�� ![]() ���ڵ�C������AC���Ե�AΪԲ�ģ�ACΪ�뾶������x�Ḻ�����ڵ�D������AD��CD��
���ڵ�C������AC���Ե�AΪԲ�ģ�ACΪ�뾶������x�Ḻ�����ڵ�D������AD��CD��
��1����֤����ABC�ա�AOD��
��2�����ACD�����ΪS����S����m�ĺ�����ϵʽ��
��3�����ı���ABCDǡ��һ��Ա�ƽ�У���m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������عˣ��ڽ�����ֵ����ʱ�����dz�����������ֵ������ȷ�����Ĵ��·�Χ��Ȼ��ͨ������С��ֵ���ڷ�Χ�ķ�����������ý�Ϊȷ����ֵ��
��������̽�����Ϊ2�������εı߳�a��ֵʱ��������̽�����̣�
1��a��2 | 1��s��4 |
1.4��a��1.5 | 1.96��s��2.25 |
1.41��a��1.42 | 1.9881��s��2.0164 |
1.414��a��1.415 | 1.999396��s��2.002225 |
����Ҳ���Խ�������ֱ�۵ؿ���������С��ֵ�Ĵ��ڷ�ͼ���Ĺ��̣�

���ַ��������ǵĽ������Ĺ����о������õ�
���������a��С��100������������֪���������������������������ȷ��a�أ�
����̽�������Dz����ɼ����ӣ���һλ������������ʼ�x��
����һ����13��a3��103����1��a��10������֪һ��һλ����������Ϊa3������ȷ��a��
�ã�13��1��23��8��33��27��43��64��53��125��63��216��73��343��83��512��93��729������ͨ����1��9�ľŸ�����������ֵȷ����������۲���Ÿ�����ֵ���ǻ��ܷ��֣����ǵĸ�λ���ָ�����ͬ��
���������103��a3��1003����10��a��100������֪һ����λ��������Ϊa3������ȷ��a�����Dz����ټ����������Ա�Ѱ�ҽ������ķ�����
����1�����һ����λ����a��������5832������ȷ��a��
��Ϊ103��5832��1003������10��a��100��a��һ����λ����
����Ϊ103��5832��203���������ǿ���ȷ��5832��ʮλ�������������ٸ��ݲ���һ���Ǿ��ܵó����ĸ�λ�������������Ӷ�ȷ�������λ������������
����2�����x��һ����λ��������x3��614125�������������Ĺ���˵����ȷ�������λ�����ķ�����
��չӦ�ã�һ�Ž������ε�С���ǵ������Ϊ2624000��m3������������Ϸ���������С���ǵİ뾶������������ʽv��![]() ��R3��
��R3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O���ң�OB=2����B=30�㣬C����AB������һ�㣨�����A��B�غϣ�������CO���ӳ�CO����O�ڵ�D������AD��
��1����AB=������������ţ���
��2������D=20��ʱ�����BOD�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com