
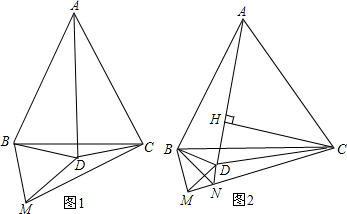
分析 (1)根据折叠的性质得到∠BDC=∠MDC,设∠ADB=x,∠ADC=y,于是得到∠BDC=∠MDC=x+y,推出∠BDM=360°-∠MDC-∠BDC=360°-2(x+y),根据等腰三角形的性质得到∠BAD=180°-2x,推出∠BAC=∠BAD+∠DAC=180°-2x+180°-2y=360°-2(x+y),于是得到结论;
(2)根据折叠的性质得到BD=MD,由于∠MDB=∠BAC=60°,得到△BMD为等边三角形,于是得到AB=BC,BD=BM,∠DBM=∠ABC=60°推出△ABD≌△CBM,根据全等三角形的性质得到∠ADB=∠CMB,CM=AD,于是得到∠ADB+∠BDN=180°,推出∠MBD+∠MND=180°,得到∠MBD+∠MND=180°,推出B,M,N,D四点共圆,根据圆周角定理得到∠BND=∠BMD=60°,截取NG=DN,于是得到△NGD是等边三角形,根据等边三角形的性质得到∠GDN=∠BDM=60°,DN=DG,得到∠BDG=∠MDN,推出△BGN≌△MND,根据全等三角形的性质得到NM=DN,BG=MN,由于BN=BG+GN=2,于是得到DN+MN=2,设AN=4x,CN=3x,求得AD=AN-DN=4x-DN,CM=CN+MN=3x+MN,求得x=2,根据直角三角形的性质即可得到结论..
解答 (1)证明:∵将△BDC向下翻折得到△MDC,
∴∠BDC=∠MDC,设∠ADB=x,∠ADC=y,
∴∠BDC=∠MDC=x+y,
∴∠BDM=360°-∠MDC-∠BDC=360°-2(x+y),
∵AB=AD,
∴∠BAD=180°-2x,
∵AB=AC=AD,
∴∠DAC=180°-2y,
∴∠BAC=∠BAD+∠DAC=180°-2x+180°-2y=360°-2(x+y),
∴∠BDM=∠BAC;
(2)解:∵将△BDC向下翻折得到△MDC,
∴BD=MD,
∵∠MDB=∠BAC=60°,
∴△BMD为等边三角形,
∴AB=BC,BD=BM,∠DBM=∠ABC=60°,
∴∠CBM=∠DBA,
在△ABD与△CBM中,
$\left\{\begin{array}{l}{AB=BC}\\{∠CBM=∠DBA}\\{BM=BD}\end{array}\right.$,
∴△ABD≌△CBM,
∴∠ADB=∠CMB,CM=AD,
∴∠ADB+∠BDN=180°,
∴∠MBD+∠MND=180°,
∵∠MBD=60°,
∴∠MND=120°,
∴∠ANC=60°,
∵∠MBD+∠MND=180°,
∴B,M,N,D四点共圆,
∴∠BND=∠BMD=60°,
截取NG=DN,连接DG,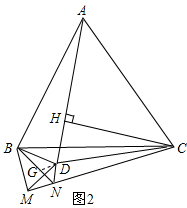 ∴△NGD是等边三角形,
∴△NGD是等边三角形,
∴∠GDN=∠BDM=60°,DN=DG,
∴∠BDG=∠MDN,
在△BGD与△MND中,
$\left\{\begin{array}{l}{BD=MD}\\{∠BDG=∠MDN}\\{DG=DN}\end{array}\right.$,
∴△BGN≌△MND,
∴NM=DN,BG=MN,
∵BN=BG+GN=2,
∴DN+MN=2,设AN=4x,CN=3x,
∴AD=AN-DN=4x-DN,CM=CN+MN=3x+MN,
∵CM=AD,
∴4x-DN=3x+MN=2,
∴x=2,
在Rt△CMH中,∵∠ANC=60°,
∴∠HCN=30°,
∴$NH=\frac{1}{2}NC$=$\frac{3}{2}$x,
∴$AH=AN-HN=4x-\frac{3}{2}x=2.5x$,
∴AH=5.
点评 本题考查了折叠的性质,全等三角形的判定和性质,等边三角形的性质,直角三角形的性质,正确的作出辅助线构造等边三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
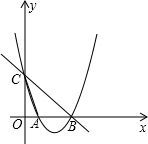 如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c经过B、C两点,且与x轴的另一个交点为A,连接AC.
如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c经过B、C两点,且与x轴的另一个交点为A,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com