

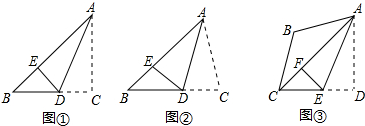
分析 (1)由折叠的性质容易得出结论;
(2)由折叠的性质得出∠1=∠2,由平行线的性质得出∠MDB=∠1,得出∠MDB=∠2,由等角对等边得出MB=MD即可;
(3)由折叠的性质得出∠2=∠1=60°,由(2)得出△MEF是等腰三角形,即可得出结论.
解答 解:(1)图a,b,c,d中∠1=∠2;理由如下:
由折叠的性质得:∠1=∠2;
(2)△MBD是等腰三角形;理由如下:
由折叠的性质得:∠1=∠2,
∵AD∥BC,
∴∠MDB=∠1,
∴∠MDB=∠2,
∴MB=MD,
∴△MBD是等腰三角形;
(3)△MEF是等边三角形,理由如下:
由折叠的性质得:∠2=∠1=60°,
由(2)得:△MEF是等腰三角形,
故△MEF是等边三角形.
点评 本题考查了翻折变换的性质、等腰三角形的判定、平行线的性质、等边三角形的判定;熟练掌握翻折变换的性质,弄清角之间的数量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 玩具型号 | A型 | B型 | C型 |
| 每名技工每天组装的数量(个) | 22 | 21 | 20 |
| 每件玩具获得的利润(元) | 8 | 10 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
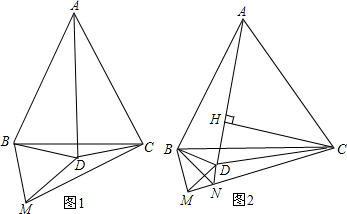
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
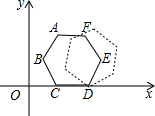 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,当点C第三次回到x轴上时,点C经过的路线长为(4+2$\sqrt{3}$)π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
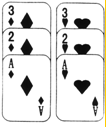 如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)
如图,是从一副扑克牌中取出的两组牌,分别是红桃1、2、3和方块1、2、3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张,求摸出的两张牌的牌面数字之和小于5的概率.(要求用列表或树状图表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com