
| 玩具型号 | A型 | B型 | C型 |
| 每名技工每天组装的数量(个) | 22 | 21 | 20 |
| 每件玩具获得的利润(元) | 8 | 10 | 6 |
分析 (1)设组装A型、B型、C型玩具的技工分别为x、y、(20-x-y)人,然后根据玩具总个数为420,列出等式,然后整理即可得到y与x的函数关系式,然后根据至少有2名技工组装同一个型号的玩具列不等式组求解即可;
(2)然后根据总利润=三种类型玩具的利润和;每种玩具的利润=玩具数量×每个玩具的利润列出函数关系式,然后根据关系进行判断即可.
解答 解:(1)设组装A型、B型、C型玩具的技工分别为x、y、(20-x-y)名.
根据题意得22x+21y+20(20-x-y)=420.
整理得y=-2x+20,
∵20-x-y=20-x-(-2x+20)=x,
∴组装A型、B型、C型玩具的技工分别为x、(-2x+20)、x名
由题意可知$\left\{\begin{array}{l}x≥2\\-2x+20≥2,x≥2\end{array}$,解得2≤x≤9,且x是整数,
(2)由题意可知:W=8×22x+10×21(-2x+20)+6×20x.
即W=-124x+4200(W是x的一次函数)
∵k=-124<0,
∴W随x的增大而减小
∵2≤x≤9,且x是整数
∴当x=2时,W的值最大.
此时W=3952(元),即最大利润为3952元.
生产分配方案如下:组装A型玩具2人,B型玩具16人,C型玩具2人.
点评 本题主要考查的是一次函数的应用,根据一次函数的性质判断出W取得最大值是x的取值是解题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
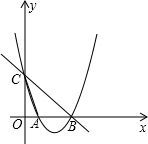 如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c经过B、C两点,且与x轴的另一个交点为A,连接AC.
如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c经过B、C两点,且与x轴的另一个交点为A,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com