
分析 (1)原式变形后,利用乘法分配律计算即可得到结果;
(2)原式合并同类项即可得到结果;
(3)原式先计算乘方运算,再计算除法运算,最后算加减运算即可得到结果;
(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(5)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(6)原式先计算乘除运算,再计算加减运算即可得到结果.
解答 解:(1)原式=(50-$\frac{1}{25}$)×(-5)=-250+$\frac{1}{5}$=-249$\frac{4}{5}$;
(2)原式=-2a+3b;
(3)原式=0-8÷(-64)-$\frac{1}{8}$=$\frac{1}{8}$-$\frac{1}{8}$=0;
(4)原式=-1-$\frac{1}{2}$×$\frac{1}{3}$×(-7)=-1+$\frac{7}{6}$=$\frac{1}{6}$;
(5)原式=-9+(12+28)÷8+299-299=-9+5=-4;
(6)原式=(-$\frac{5}{3}$+$\frac{5}{2}$)×$\frac{6}{5}$=-2+3=1.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
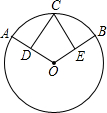 如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一点,CD=CE.
如图,在⊙O中,D、E分别是半径OA、OB的中点,C是⊙O上一点,CD=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com