
【题目】某中学欲开设A实心球、B立定跳远、C跑步、D足球四种体育活动,为了了解学生们对这些项目的选择意向,随机抽取了部分学生,并将调查结果绘制成图1、图2,请结合图中的信息,解答下列问题:
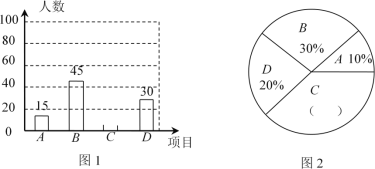
(1)本次共调查了 名学生;
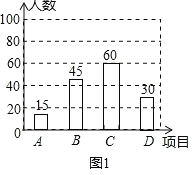
(2)将条形统计图补充完整;
(3)求扇形![]() 的圆心角的度数;
的圆心角的度数;
(4)某班喜欢“跑步”的学生有4名,其中有2名男生,2名女生,现从这4名学生中选取2名,请用画树状图或列表的方法,求出刚好抽到同性的概率。
【答案】(1)150(2)条形图见解析(3)![]() ; (4)
; (4)![]() .
.
【解析】
(1)从两个统计图可得,“![]() 组”的有15人,占调查人数的
组”的有15人,占调查人数的![]() ,可求出调查人数;
,可求出调查人数;
(2)求出“![]() 组”人数,即可补全条形统计图:
组”人数,即可补全条形统计图:
(3)样本中,“![]() 组”占
组”占![]() ,因此圆心角占
,因此圆心角占![]() 的
的![]() ,可求出度数;
,可求出度数;
(4)用列表法列举出所有可能出现的结果,从中找出“同性”的结果数,进而求出概率.
(1)![]() (人).
(人).
故答案为150
(2)![]() (人),补全条形如图所示
(人),补全条形如图所示
(3)![]()
答:扇形![]() 的圆心角的度数
的圆心角的度数![]() ;
;
(4)用列表法表示所有可能出现的结果如下
第2人 第1人 | 男1 | 男2 | 女 |
男1 | 男1男2 | 男1女 | |
男2 | 男2男1 | 男2女 | |
女 | 女男1 | 女男2 |
共有6种可能出现的结果,其中一男一女的有4种,故刚好抽到一男一女的概率为
![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边AB上求作一点P,使PC=PB,并连接PC;(不写作法,保留作图痕迹)
(2)当AC=3,BC=4时,△ACP的周长= ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=![]() AC;
AC;
(2)变式求异 如图2,若∠C=90°,m=6![]() ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: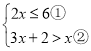 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(1)解不等式①,得: ;
(2)解不等式②得: ;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D是边BC上一动点(不与B、C重合),
,点D是边BC上一动点(不与B、C重合),![]() ,DE交AC于点E,且
,DE交AC于点E,且![]() .下列结论:①
.下列结论:①![]() ∽
∽![]() ;②当
;②当![]() 时,
时,![]() 与
与![]() 全等;③
全等;③![]() 为直角三角形时,BD等于8或
为直角三角形时,BD等于8或![]() .其中正确的有__________.(选填序号)
.其中正确的有__________.(选填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
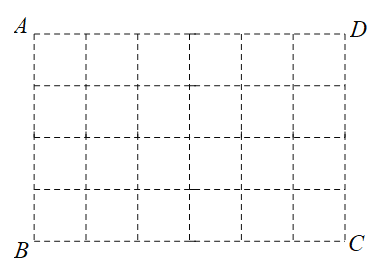
【题目】如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.
(1)在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH;
(2)在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件40元的商品,经调查发现,该商品每天的销售量![]() (件
(件![]() 与销售单价
与销售单价![]() (元
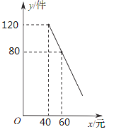
(元![]() 之间满足一次函数关系,其图象如图所示.
之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(2)若商店要使销售该商品每天获得的利润等于1000元,每天的销售量应为多少件?
(3)若商店按单价不低于成本价,且不高于65元销售,则销售单价定为多少元时,才能使销售该商品每天获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.动点P从点A出发,沿AB以每秒5个单位长度的速度向终点B运动.当点P不与点A重合时,过点P作PD⊥AC于点D、PE∥AC,过点D作DE∥AB,DE与PE交于点E.设点P的运动时间为t秒.
(1)线段AD的长为 .(用含t的代数式表示).
(2)当点E落在BC边上时,求t的值.
(3)设△DPE与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式.
(4)若线段PE的中点为Q,当点Q落在△ABC一边垂直平分线上时,直接写出t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com