
 如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是
如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是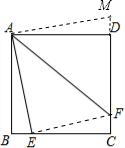 解:如图,延长CD到M,使DM=BE,
解:如图,延长CD到M,使DM=BE,
|
|


科目:初中数学 来源: 题型:
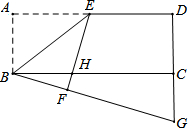 已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH=
已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-
如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | ★ | △ | x | -6 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
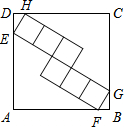 如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为
如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为查看答案和解析>>
科目:初中数学 来源: 题型:
| 加数的个数(n) | 和(S) |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
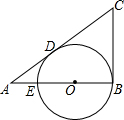 已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( )
已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( )| A、96 | B、48 | C、36 | D、24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com