
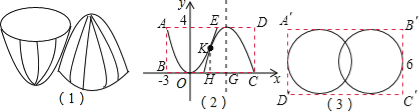
【题目】超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板( )平方厘米.(不计重合部分)

A. 253 B. 288 C. 206 D. 245
【答案】A
【解析】
试题图,“喜之郎”果冻礼盒是一长方体.2个底面为矩形A′B′C′D′(如图3),2个侧面为矩形ABCD(如图2),2个侧面是以AB为高,AE为底的矩形.
解:建立如图(2)所示的平面直角坐标系,过切点K作KH⊥OD于点H.
依题意知K(x,2).
易求开口向上抛物线的解析式:y=![]() x2,
x2,
所以2=![]() x2,
x2,
解得x=![]() 或x=﹣
或x=﹣![]() (舍去),
(舍去),
∴OH=HG=![]() ,
,
∴BC=BO+OH+HG+GC=3+![]() +
+![]() +3=6+3
+3=6+3![]() ,
,
∴S矩形ABCD=ABBC=4×(6+3![]() )=24+12
)=24+12![]() (平方厘米).
(平方厘米).
如图3,S矩形A′B′C′D′=6BC=6×(6+3![]() )(平方厘米).
)(平方厘米).
所以,2S矩形ABCD+2S矩形A′B′C′D′+2ABAE=178+80![]() (平方厘米).
(平方厘米).
2×(24+12![]() )+2×(36+18
)+2×(36+18![]() )+2×4×6=168+60
)+2×4×6=168+60![]() ≈253(平方厘米).
≈253(平方厘米).
故选:A.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
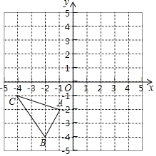
【题目】如图,在平面直角坐标系中,![]() 的三个顶点分别为
的三个顶点分别为![]() ,
,![]() ,
,![]() .
.
![]() 把
把![]() 向上平移
向上平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
![]() 已知点
已知点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,请画出直线
成轴对称,请画出直线![]() 及
及![]() 关于直线
关于直线![]() 对称的
对称的![]() .
.
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 距离之和最小,请直接写出
距离之和最小,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示,直线l经过点(0,1),并且与x轴平行,△A1B1C1与△ABC关于直线l对称.
(1)画出三角形A1B1C1;
(2)若点P(m,n)在AC边上,则点P关于直线l的对称点P1的坐标为 ;
(3)在直线l上画出点Q,使得QA+QC的值最小.
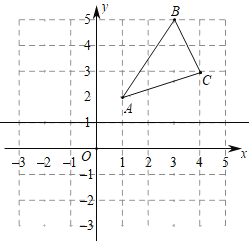
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
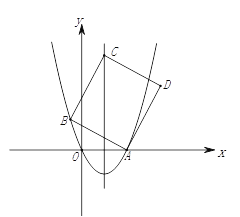
【题目】如图,抛物线![]() 交x轴的正半轴于点A,点B(
交x轴的正半轴于点A,点B(![]() ,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
(1)求a的值及点A的坐标;
(2)当点D恰好落在抛物线上时,求n的值;
(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n=___________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列题目的解题过程:
已知![]() 为
为![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴![]() 是直角三角形
是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ;
(2)该步正确的写法应是: ;
(3)本题正确的结论为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
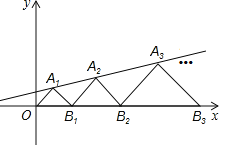
【题目】如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=![]() x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com