
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示,直线l经过点(0,1),并且与x轴平行,△A1B1C1与△ABC关于直线l对称.
(1)画出三角形A1B1C1;
(2)若点P(m,n)在AC边上,则点P关于直线l的对称点P1的坐标为 ;
(3)在直线l上画出点Q,使得QA+QC的值最小.
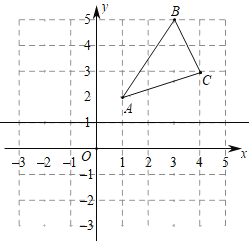
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
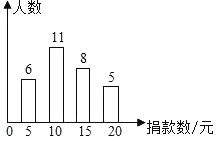
(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.
(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;
(2)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w元最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
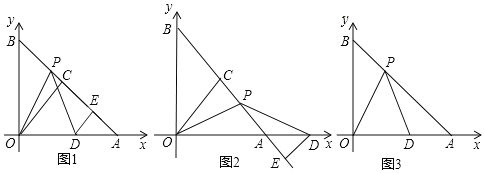
【题目】已知,在平面直角坐标系中,![]() 、
、![]() ,m、n满足
,m、n满足![]() .C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)如图1,当点P在线段AB上运动时,点D恰在线段OA上,则PE与AB的数量关系为 .
(2)如图2,当点D在点A右侧时,(1)中结论是否成立?若成立,写出证明过程;若不成立,说明理由.
(3)设AB=5![]() ,若∠OPD=45°,直接写出点D的坐标.
,若∠OPD=45°,直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
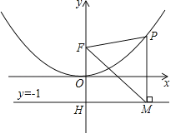
【题目】二次函数图象的顶点在原点O,且经过点A(1,![]() );点F(0,1)在y轴上.直线y=-1与y轴交于点H.
);点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:点M到∠OFP两边距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(基础模型)
已知等腰直角△ABC,∠ACB=90°,AC=CB,过点C任作一条直线l(不与CA、CB重合),过点A作AD⊥l于D,过点B作BE⊥l于 E.
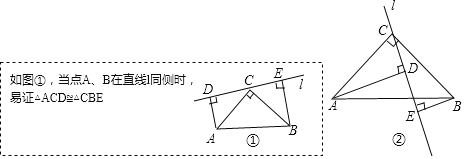
(1)如图②,当点A、B在直线l异侧时,求证:△ACD≌△CBE
(模型应用)
在平面直角坐标性xOy中,已知直线l:y=kx﹣4k(k为常数,k≠0)与x轴交于点A,与y轴的负半轴交于点 B.以AB为边、B为直角顶点作等腰直角△ABC.
(2)若直线l经过点(2,﹣3),当点C在第三象限时,点C的坐标为 .
(3)若D是函数y=x(x<0)图象上的点,且BD∥x轴,当点C在第四象限时,连接CD交y轴于点E,则EB的长度为 .
(4)设点C的坐标为(a,b),探索a,b之间满足的等量关系,直接写出结论.(不含字母k)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板( )平方厘米.(不计重合部分)

A. 253 B. 288 C. 206 D. 245
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随机抽取某小吃店一周的营业额(单位:元)如下表:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
540 | 680 | 640 | 640 | 780 | 1110 | 1070 | 5460 |
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元.
(2)估计一个月的营业额(按30天计算):
①星期一到星期五营业额相差不大,用这5天的平均数估算合适么: .(填“合适”或“不合适”)
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com