
����Ŀ��������ģ�ͣ�
��֪����ֱ�ǡ�ABC����ACB��90�㣬AC��CB������C����һ��ֱ��l������CA��CB�غϣ�������A��AD��l��D������B��BE��l�� E��
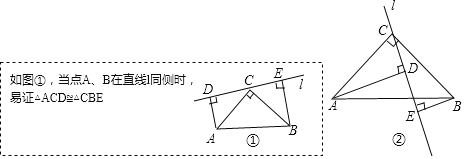
��1����ͼ��������A��B��ֱ��l���ʱ����֤����ACD�ա�CBE
��ģ��Ӧ�ã�
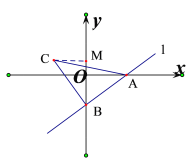
��ƽ��ֱ��������xOy�У���ֱ֪��l��y��kx��4k��kΪ������k��0����x�ύ�ڵ�A����y��ĸ����ύ�ڵ� B����ABΪ�ߡ�BΪֱ�Ƕ���������ֱ�ǡ�ABC��
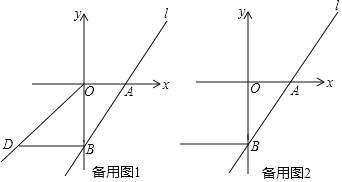
��2����ֱ��l�����㣨2����3��������C�ڵ�������ʱ����C������Ϊ�� ����
��3����D�Ǻ���y��x��x��0��ͼ���ϵĵ㣬��BD��x�ᣬ����C�ڵ�������ʱ������CD��y���ڵ�E����EB�ij���Ϊ�� ����
��4�����C������Ϊ��a��b����̽��a��b֮������ĵ�����ϵ��ֱ��д�����ۣ���������ĸk��
���𰸡���1�������������2��(��6����2)����3��2����4��a+ b=-4��b��a��4��
��������
��1������ͬ�ǵ��������жϳ���CAD����BCE����������AAS���ɵó����ۣ�
��2�������ֱ��l�Ľ���ʽ������ȷ������A��B���꣬���жϳ���ACD�ա�CBE�����ɵó����ۣ�
��3��ͬ��2���ķ����ɵá�OAB�ա�FBC���Ӷ���BF��OA��4����֤��BED�ա�FEC��AAS�������ɵõ��𰸣�
��4���ֵ�C�ڵڶ����ޣ��������͵������������������ȷ������A��B���꣬��ͬ��2����3���ķ���ȷ������C�����꣨��k��ʾ�������ɵó����ۣ�
��1���ߡ�ACB��90�㣬
���ACD+��ECB��90�㣬
��AD��l��BE��l��
���ADC����BEC��90�㣬
���ACD+��CAD����ACD+��BCE��90�㣬
���CAD����BCE��
��CA��CB��
���ACD�ա�CBE��AAS����
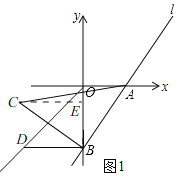
��2����ͼ1������C��CE��y���ڵ�E��
��ֱ��l��y��kx��4k������(2����3)��
��2k��4k����3��
��k��![]() ��
��
��ֱ��l�Ľ���ʽΪ��y��![]() x��6��
x��6��
��x��0����y����6��
��B(0����6)��
��OB��6��
��y��0����0��![]() x��6��
x��6��
��x��4��
��A(4��0)��
��OA��4��
ͬ��1���ķ����ã���OAB�ա�EBC��AAS����
��CE��OB��6��BE��OA��4��
��OE��OB��BE��6��4��2��
�ߵ�C�ڵ������ޣ�
��C(��6����2)��
�ʴ�Ϊ��(��6����2)��
��3����ͼ2��
����ֱ��l��y��kx��4k��
��x��0����y����4k��
��B(0����4k)��
��OB��4k��
��y��0����kx��4k��0��
��x��4��
��A(4��0)��
��OA��4��
����C��CF��y����F�����OAB�ա�FBC��AAS����
��BF��OA��4��CF��OB��4k��
��OF��OB+BF��4k+4��
�ߵ�C�ڵ������ޣ�
��C(4k��-4k-4)��
��B(0����4k)��
��BD��x�ᣬ��D��y��x�ϣ�
��D(��4k����4k)��
��BD��4k��CF��
��CF��y����F��
���CFE��90�㣬
��BD��x�ᣬ
���DBE��90�㣽��CFE��
�ߡ�BED����FEC��
���BED�ա�FEC��AAS����
��BE��EF��![]() BF��2��
BF��2��
�ʴ�Ϊ��2��
��4���ٵ���C�ڵ�������ʱ���ɣ�3��֪��C(4k��-4k-4)��
��C(a��b)��
��a��4k��b��-4k-4��
��a+ b=-4��
�ڵ���C�ڵ�������ʱ���ɣ�3��֪��B(0����4k)��A(4��0)��
��OB��4k��OA��4��
��ͼ1���ɣ�2��֪����OAB�ա�EBC��AAS����
��CE��OB��4k��BE��OA��4��
��OE��OB��BE��4k��4��
��C(��4k��-4k+4)��
��C(a��b)��
��a����4k��b��-4k+4��
��b��a��4��
�۵���C�ڵڶ�����ʱ����ͼ3���ɣ�3��֪��B(0����4k)��A(4��0)��
��OB��4k��OA��4��
�ߡ�OAB�ա�MBC��AAS����
��CM��OB��4k��BM��OA��4��
��OM��BM��BO��4��4k��
��C(��4k��4��4k)��
��C(a��b)��
��a����4k��b��4��4k��
��b��a��4��
�ܵ�C�������ڵ�һ���ޣ�
����������a+ b=-4��b��a��4��
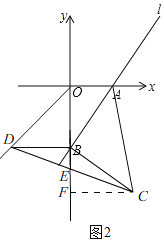
ͼ3


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
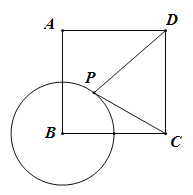
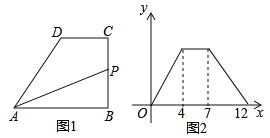
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4����B�İ뾶Ϊ2����P�ǡ�B�ϵ�һ�����㣬��PD��![]() PC�����ֵΪ_____��
PC�����ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����ѧ��ÿ����У�������ʱ�䣨��λ��h������������˸�У�IJ��ֳ���ѧ�������ݵ����������Ƴ����µ�ͳ��ͼ�ٺ�ͼ�ڣ�����������Ϣ������������⣺
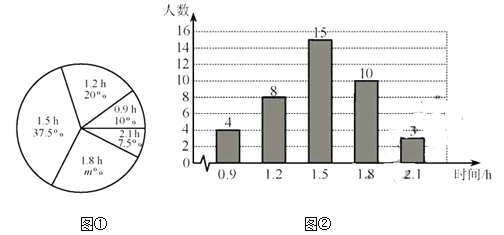
�����ν��ܵ���ij���ѧ������Ϊ___________��ͼ����m��ֵΪ_____________��
������ͳ�Ƶ�����ÿ����У�����ʱ�����ݵ�ƽ��������������λ����
������ͳ�Ƶ�����ÿ����У�����ʱ����������ݣ�����У����800������ѧ�������Ƹ�Уÿ����У�����ʱ�����1h��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
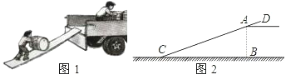
����Ŀ����ͼ1�ǹ��˽���������ϻ������õķ�������һ��ľ��б���ڻ��������β�����γ�һ��б�£�����ͨ��б�½��а��ˣ����ݾ��飬ľ�������ļн�Ϊ20��(��ͼ2�С�ACB��20��)ʱ��Ϊ���ʣ���֪��������ײ�������ľ���AB��1.5m��ľ�峬�����Ჿ��AD��0.5m�������ľ��CD�ij��ȣ�
(�ο����ݣ�sin20���0.3420��cos20���0.9397����ȷ��0.1m)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ABC��λ����ͼ��ʾ��ֱ��l�����㣨0��1����������x��ƽ�У���A1B1C1���ABC����ֱ��l�Գƣ�
��1������������A1B1C1��
��2������P��m��n����AC���ϣ����P����ֱ��l�ĶԳƵ�P1������Ϊ�� ����
��3����ֱ��l�ϻ�����Q��ʹ��QA+QC��ֵ��С��
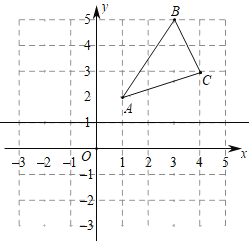
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() �ķ����˶��������
�ķ����˶��������![]() ֹͣ�����
ֹͣ�����![]() �˶���·��Ϊ
�˶���·��Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() �����
�����![]() ��
��![]() �ĺ���ͼ����ͼ2��ʾ����ô
�ĺ���ͼ����ͼ2��ʾ����ô![]() �ߵij���Ϊ______.
�ߵij���Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�һ����ϵ���״�����������ABC����BC=120mm����AD=80mm�������ӹ��������������ͼ1��ʹ�����ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ�

��1����֤����AEF�ס�ABC��
��2�����������������ı߳���
��3����������ӹ��ɾ��������ͼ2����������ε��������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
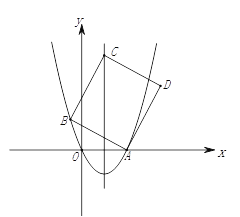
����Ŀ����ͼ��������![]() ��x����������ڵ�A����B��
��x����������ڵ�A����B��![]() ��a�����������ϣ���C�������߶Գ����ϵ�һ�㣬����AB��BC����AB��BCΪ�ڱ�����ABCD���ǵ�C������Ϊn��
��a�����������ϣ���C�������߶Գ����ϵ�һ�㣬����AB��BC����AB��BCΪ�ڱ�����ABCD���ǵ�C������Ϊn��
��1����a��ֵ����A�����ꣻ
��2������Dǡ��������������ʱ����n��ֵ��
��3����CD�������ߵĽ���ΪE������AE��BE������AEB�����Ϊ7ʱ��n=___________����ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() �ֱ��DZ�
�ֱ��DZ�![]() ���е㣬�ӳ�
���е㣬�ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() �����ı���
�����ı���![]() .��ʹ�ı���
.��ʹ�ı���![]() �������Σ���Ӧ��
�������Σ���Ӧ��![]() ��������һ������Ϊ__________.
��������һ������Ϊ__________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com