
【题目】已知,在平面直角坐标系中,![]() 、
、![]() ,m、n满足
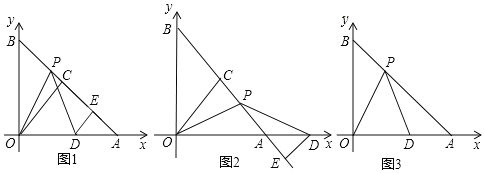
,m、n满足![]() .C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)如图1,当点P在线段AB上运动时,点D恰在线段OA上,则PE与AB的数量关系为 .
(2)如图2,当点D在点A右侧时,(1)中结论是否成立?若成立,写出证明过程;若不成立,说明理由.
(3)设AB=5![]() ,若∠OPD=45°,直接写出点D的坐标.
,若∠OPD=45°,直接写出点D的坐标.
【答案】(1)AB=2PE;(2)成立,理由见解析;(3)点D![]() .
.
【解析】
(1)根据非负数的性质分别求出m、n,证明△POC≌△DPE,可得出OC=PE,由AB=2OC,则结论得出;
(2)根据等腰直角三角形的性质得到∠AOC=∠BOC=45°,OC⊥AB,证明△POC≌△DPE,根据全等三角形的性质得到OC=PE,可得到答案;
(3)证明△POB≌△DPA,得到PA=OB=5,DA=PB,根据坐标与图形性质解答即可.
解:(1)∵(m﹣n)2+|m﹣5|=0,
∴m﹣n=0,m﹣5=0,
∴m=n=5,
∴A(5,0)、B(0,5),
∴AC=BC=5,
∴△AOB为等腰直角三角形,
∴∠AOC=∠BOC=45°,OC⊥AB,
∵PO=PD,
∴∠POD=∠PDO,
∵D是x轴正半轴上一点,
∴点P在BC上,
∵∠POD=45°+∠POC,∠PDO=45°+∠DPE,
∴∠POC=∠DPE,
在△POC和△DPE中,
 ,在此处键入公式。
,在此处键入公式。
∴△POC≌△DPE(AAS),
∴OC=PE,
∵C为AB的中点,
∴AB=2OC,
∴AB=2PE.
故答案为:AB=2PE.
(2)成立,理由如下:
∵点C为AB中点,
∴∠AOC=∠BOC=45°,OC⊥AB,
∵PO=PD,
∴∠POD=∠PDO,
∵∠POD=45°﹣∠POC,∠PDO=45°﹣∠DPE,
∴∠POC=∠DPE,
在△POC和△DPE中,
 ,
,
∴△POC≌△DPE(AAS),
∴OC=PE,
又∠AOC=∠BAO=45°
∴OC=AC=AB
∴AB=2PE;
(3)∵AB=5![]() ,
,
∴OA=OB=5,
∵OP=PD,
∴∠POD=∠PDO=![]() =67.5°,
=67.5°,
∴∠APD=∠PDO﹣∠A=22.5°,∠BOP=90°﹣∠POD=22.5°,
∴∠APD=∠BOP,
在△POB和△DPA中,
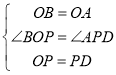 ,
,
∴△POB≌△DPA(SAS),
∴PA=OB=5,DA=PB,
∴DA=PB=5![]() ﹣5,
﹣5,
∴OD=OA﹣DA=5﹣(5![]() ﹣5)=10﹣5
﹣5)=10﹣5![]() ,
,
∴点D的坐标为![]() .
.


科目:初中数学 来源: 题型:
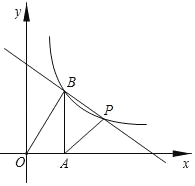
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
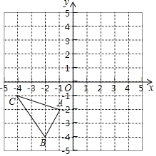
【题目】如图,在平面直角坐标系中,![]() 的三个顶点分别为
的三个顶点分别为![]() ,
,![]() ,
,![]() .
.
![]() 把
把![]() 向上平移
向上平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
![]() 已知点
已知点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,请画出直线
成轴对称,请画出直线![]() 及
及![]() 关于直线
关于直线![]() 对称的
对称的![]() .
.
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 距离之和最小,请直接写出
距离之和最小,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
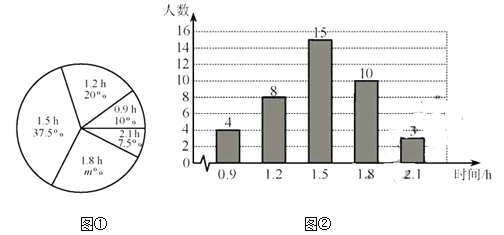
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
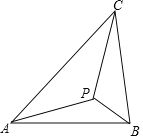
A.5 B.4 C.3+![]() D.2+
D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
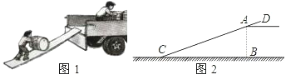
【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示,直线l经过点(0,1),并且与x轴平行,△A1B1C1与△ABC关于直线l对称.
(1)画出三角形A1B1C1;
(2)若点P(m,n)在AC边上,则点P关于直线l的对称点P1的坐标为 ;
(3)在直线l上画出点Q,使得QA+QC的值最小.
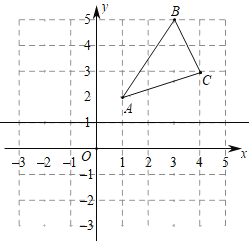
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列题目的解题过程:
已知![]() 为
为![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴![]() 是直角三角形
是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ;
(2)该步正确的写法应是: ;
(3)本题正确的结论为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com