
【题目】抛物线y=ax2+bx+3经过点A(1,0)和点B(5,0).
(1)求该抛物线所对应的函数解析式;
(2)该抛物线与直线y= ![]() x+3相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.
x+3相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.
①连结PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
②连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
【答案】
(1)
解:∵抛物线y=ax2+bx+3经过点A(1,0)和点B(5,0),
∴ ![]() ,解得
,解得 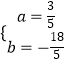 ,
,
∴该抛物线对应的函数解析式为y= ![]() x2﹣
x2﹣ ![]() x+3
x+3
(2)
解:①∵点P是抛物线上的动点且位于x轴下方,
∴可设P(t, ![]() t2﹣
t2﹣ ![]() t+3)(1<t<5),
t+3)(1<t<5),
∵直线PM∥y轴,分别与x轴和直线CD交于点M、N,
∴M(t,0),N(t, ![]() t+3),
t+3),
∴PN= ![]() t+3﹣(
t+3﹣( ![]() t2﹣
t2﹣ ![]() t+3)=﹣
t+3)=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]()
联立直线CD与抛物线解析式可得  ,解得
,解得 ![]() 或
或 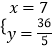 ,
,
∴C(0,3),D(7, ![]() ),
),
分别过C、D作直线PN的直线,垂足分别为E、F,如图1,
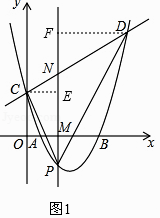
则CE=t,DF=7﹣t,
∴S△PCD=S△PCN+S△PDN= ![]() PNCE+
PNCE+ ![]() PNDF=
PNDF= ![]() PN=
PN= ![]() [﹣
[﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ]=﹣
]=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,△PCD的面积有最大值,最大值为
时,△PCD的面积有最大值,最大值为 ![]()
②存在.
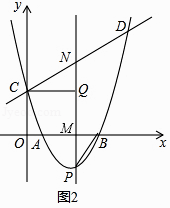
∵∠CQN=∠PMB=90°,
∴当△CNQ与△PBM相似时,有 ![]() =
= ![]() 或
或 ![]() =
= ![]() 两种情况,
两种情况,
∵CQ⊥PM,垂足为Q,
∴Q(t,3),且C(0,3),N(t, ![]() t+3),
t+3),
∴CQ=t,NQ= ![]() t+3﹣3=
t+3﹣3= ![]() t,
t,
∴ ![]() =
= ![]() ,
,
∵P(t, ![]() t2﹣
t2﹣ ![]() t+3),M(t,0),B(5,0),
t+3),M(t,0),B(5,0),
∴BM=5﹣t,PM=0﹣( ![]() t2﹣
t2﹣ ![]() t+3)=﹣
t+3)=﹣ ![]() t2+
t2+ ![]() t﹣3,
t﹣3,
当 ![]() =
= ![]() 时,则PM=
时,则PM= ![]() BM,即﹣
BM,即﹣ ![]() t2+
t2+ ![]() t﹣3=
t﹣3= ![]() (5﹣t),解得t=2或t=5(舍去),此时P(2,
(5﹣t),解得t=2或t=5(舍去),此时P(2, ![]() );
);
当 ![]() =
= ![]() 时,则BM=
时,则BM= ![]() PM,即5﹣t=
PM,即5﹣t= ![]() (﹣
(﹣ ![]() t2+
t2+ ![]() t﹣3),解得t=
t﹣3),解得t= ![]() 或t=5(舍去),此时P(
或t=5(舍去),此时P( ![]() ,﹣
,﹣ ![]() );
);
综上可知存在满足条件的点P,其坐标为(2, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)由A、B两点的坐标,利用待定系数法可求得抛物线解析式;(2)①可设出P点坐标,则可表示出M、N的坐标,联立直线与抛物线解析式可求得C、D的坐标,过C、D作PN的垂线,可用t表示出△PCD的面积,利用二次函数的性质可求得其最大值;②当△CNQ与△PBM相似时有 ![]() =
= ![]() 或
或 ![]() =
= ![]() 两种情况,利用P点坐标,可分别表示出线段的长,可得到关于P点坐标的方程,可求得P点坐标.
两种情况,利用P点坐标,可分别表示出线段的长,可得到关于P点坐标的方程,可求得P点坐标.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).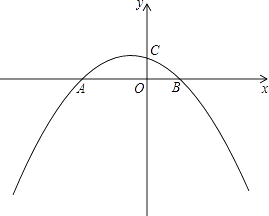
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN﹣CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中,∠BAO=90°,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
(1)如图1,若点B在OP上,则
①ACOE(填“<”,“=”或“>”);
②线段CA、CO、CD满足的等量关系式是;
(2)将图1中的等腰Rt△ABO绕O点顺时针旋转α(0°<α<45°),如图2,那么(1)中的结论②是否成立?请说明理由;
(3)将图1中的等腰Rt△ABO绕O点顺时针旋转α(45°<α<90°),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈ ![]() ,cos53°≈
,cos53°≈ ![]() ,tan53°≈
,tan53°≈ ![]() ,
, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性.
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果. 
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.①
B.②
C.①②
D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】舟山市2010﹣2014年社会消费品零售总额及增速统计图如图: 
请根据图中信息,解答下列问题:
(1)求舟山市2010﹣2014年社会消费品零售总额增速这组数据的中位数.
(2)求舟山市2010﹣2014年社会消费品零售总额这组数据的平均数.
(3)用适当的方法预测舟山市2015年社会消费品零售总额(只要求列式说明,不必计算出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com