
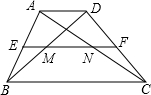
 如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长.
如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 15 |
| 16 |
| 1 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
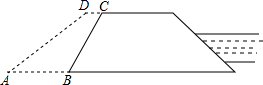 由于发生大洪水,需要加固一段大堤,计划使大堤加宽1m,使坡度由原来的1:2变成1:3.已知原来BC=12m,堤长100m,那么需要砂石和土多少立方米?
由于发生大洪水,需要加固一段大堤,计划使大堤加宽1m,使坡度由原来的1:2变成1:3.已知原来BC=12m,堤长100m,那么需要砂石和土多少立方米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com