
 如图,两双曲线y=
如图,两双曲线y=| k |
| x |
| 3 |
| x |
| 3 |
| x |
| k |
| x |
| k |
| x |
| 4 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
| k |
| x |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| x |
| 4 |
| x |
| 4 |
| x |
| 3 |
| x |
| 7 |
| x |
| 1 |
| 2 |
| 7 |
| x |


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
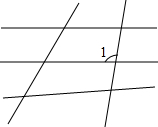 在图中,先标上适当的字母,再回答下列问题;
在图中,先标上适当的字母,再回答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=
如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=| 4 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证:
如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证:| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-
如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
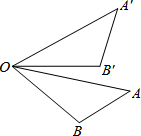 如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )
如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )| A、4sin22° |
| B、2sin44° |
| C、4cos22° |
| D、2cos44° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com