
 如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.
如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S.
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S.| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
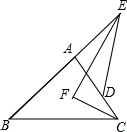 如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=
如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,两双曲线y=
如图,两双曲线y=| k |
| x |
| 3 |
| x |
| 3 |
| x |
| k |
| x |
| k |
| x |
| 4 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 “五•一”节,某超市开展“有奖促销”活动,凡购物不少于30元的顾客均有一次转动转盘的机会(如图,转盘被分为8个全等的小扇形),当指针最终指向数字8时,该顾客获一等奖;当指针最终指向3或5时,该顾客获二等奖(若指针指向分界线则重转). 经统计,当天发放一、二等奖奖品共600份,那么据此估计参与此次活动的顾客为
“五•一”节,某超市开展“有奖促销”活动,凡购物不少于30元的顾客均有一次转动转盘的机会(如图,转盘被分为8个全等的小扇形),当指针最终指向数字8时,该顾客获一等奖;当指针最终指向3或5时,该顾客获二等奖(若指针指向分界线则重转). 经统计,当天发放一、二等奖奖品共600份,那么据此估计参与此次活动的顾客为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com