
 如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-
如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-| 3 |
| PM |
| BM |
| 3 |
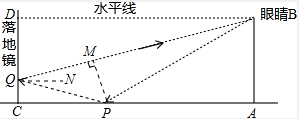 解:过点P作PM⊥BQ于点M,过点Q作QN∥AC,
解:过点P作PM⊥BQ于点M,过点Q作QN∥AC,| PM |
| BM |
| 3 |
| 3 |
| 3 |
16+16
| ||
| 15 |
16+16
| ||
| 15 |
16+16
| ||
| 15 |
| 3 |
16
| ||
| 15 |
16
| ||
| 15 |
32
| ||
| 15 |
32
| ||
| 15 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
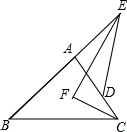 如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=
如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,两双曲线y=
如图,两双曲线y=| k |
| x |
| 3 |
| x |
| 3 |
| x |
| k |
| x |
| k |
| x |
| 4 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| A、只有①② | B、只有①③ |
| C、只有②③ | D、①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB、CD于点E、F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O任作一条直线分别交AB、CD于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:
 “五•一”节,某超市开展“有奖促销”活动,凡购物不少于30元的顾客均有一次转动转盘的机会(如图,转盘被分为8个全等的小扇形),当指针最终指向数字8时,该顾客获一等奖;当指针最终指向3或5时,该顾客获二等奖(若指针指向分界线则重转). 经统计,当天发放一、二等奖奖品共600份,那么据此估计参与此次活动的顾客为
“五•一”节,某超市开展“有奖促销”活动,凡购物不少于30元的顾客均有一次转动转盘的机会(如图,转盘被分为8个全等的小扇形),当指针最终指向数字8时,该顾客获一等奖;当指针最终指向3或5时,该顾客获二等奖(若指针指向分界线则重转). 经统计,当天发放一、二等奖奖品共600份,那么据此估计参与此次活动的顾客为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com