
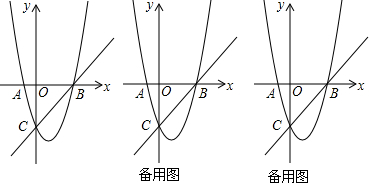
分析 (1)根据自变量与函数值的对应关系,可得C、B点坐标,根据待定系数法,可得函数解析式;
(2)根据等腰直角三角形的判定与性质,可得AD与DE的关系,根据解方程,可得答案;
(3)根据相似三角形的判定与性质,可得$\frac{EG}{GH}$=$\frac{EF}{FP}$=$\frac{5}{1}$,根据解方程,可用a表示P点的坐标,根据P在抛物线的图象上,可得关于a的方程,把a的值代入P点坐标,可得答案.
解答 解:(1)抛物线y=ax2-2x-3当x=0时,y=-3,即C(0,-3),
将C代入直线y=x+b,得b=-3,即直线的解析式为y=x-3,
当y=0时,x-3=0,解得x=3,即B点坐标(3,0).
将B点坐标代入抛物线的解析式,得
9a-6-3=0,
解得a=1,
抛物线的解析式为y=x2-2x-3;
(2)如图1: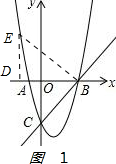 ,
,
设E点的坐标为(m,m2-2m-3),
过E作ED⊥x轴于D点,OB=OC,∠OBC=45°.
∵BE⊥BC,
∴∠EBD=45°,
BD=ED,即3-m=m2-2m-3,
解得m=-2,m=3(不符合题意的解要舍去),
m2-2m-3=(-2)2-2×(-2)-3=5,
即E(-2,5)
(3)如图2: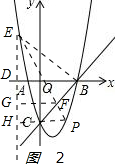 ,
,
过F作FG⊥ED于G点,过P作PH⊥ED于H,PH∥CF,
△EGF∽△EHP,
$\frac{EF}{FP}$=$\frac{EG}{GH}$=$\frac{FG}{PH-FG}$.
设F(a,a-3),S△ECF=5S△CPF时,$\frac{EF}{FP}$=$\frac{5}{1}$.
EG=5-(a-3)=8-a,GH=a-3-y,
$\frac{EG}{GH}$=$\frac{EF}{FP}$=$\frac{5}{1}$,即$\frac{8-a}{a-3-y}$=$\frac{5}{1}$,
解得y=$\frac{6a-23}{5}$,
同理可得,x=$\frac{6a+2}{5}$,即P($\frac{6a+2}{5}$,$\frac{6a-23}{5}$),
将P代入抛物线的解析式,得$\frac{6a-23}{5}$=($\frac{6a+2}{5}$)2-2×$\frac{6a+2}{5}$-3,
化简,得6a2-11a+4=0,
解得a=$\frac{4}{3}$或a=$\frac{1}{2}$.
当a=$\frac{4}{3}$时,x=$\frac{6×\frac{4}{3}+2}{5}$=2,
当a=$\frac{1}{2}$时,x=$\frac{6×\frac{1}{2}+2}{5}$=1.
综上所述:点P的横坐标为2或1.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,(2)利用等腰直角三角形的判定与性质得出关于m的方程是解题关键;(3)利用了相似三角形的判定与性质,利用相似三角形的性质得出P点坐标用a表示出来是解题关键.


科目:初中数学 来源: 题型:解答题
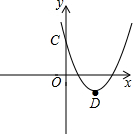 已知二次函数y=x2-2mx+m2-1(m≠0)的图象经过点(1,0).
已知二次函数y=x2-2mx+m2-1(m≠0)的图象经过点(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
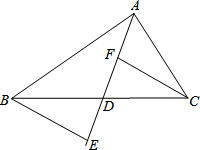 如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.
如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
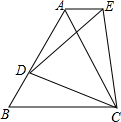 如图,等边△ABC中,D是AB边上的动点,以CD为一边向上作等边△EDC,连接AE.(1)求证:AE∥BC.
如图,等边△ABC中,D是AB边上的动点,以CD为一边向上作等边△EDC,连接AE.(1)求证:AE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com