
【题目】如图,在数轴上A点表示数a,B点表示数b,且a、b满足|a+2|+(b6)2=0![]()
(1)点A表示的数为 ;点B表示的数为 ;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=3BC,则C点表示的数 ;
(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请分别表示出甲、乙两小球到原点的距离(用t表示).
【答案】(1)2、6;(2)4或10;(3)当0<t3时,乙到原点的距离:62t(0t3);当t>3时,乙球到原点的距离为:2t6(t>3).
【解析】
(1)根据非负数的性质求得a=-2,b=6;
(2)分C点在线段AB上和线段AB的延长线上两种情况讨论即可求解;
(3)甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,此时OB的长度-乙球运动的路程即为乙球到原点的距离;(Ⅱ)当t>3时,乙球从原点O处开始向右运动,此时乙球运动的路程-OB的长度即为乙球到原点的距离.
(1)∵|a+2|+|b6|=0,
∴a+2=0,b6=0,
解得,a=2,b=6,
∴点A表示的数为2,点B表示的数为6.
故答案为:2、6;
(2)设数轴上点C表示的数为c.
∵AC=3BC,
∴|ca|=3|cb|,即|c+2|=3|c6|.
∵AC=3BC>BC,
∴点C不可能在BA的延长线上,则C点可能在线段AB上和线段AB的延长线上。
①当C点在线段AB上时,则有2c6,
得c+2=3(6c),解得c=4;
②当C点在线段AB的延长线上时,则有c>6,
得c+2=3(c6),解得c=10.
故当AC=3BC时,c=4或c=10;
故答案为:4或10;
(3)∵甲球运动的路程为:1t=t,OA=2,
∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:
①当0<t3时,乙球从点B处开始向左运动,一直到原点O,
∵OB=6,乙球运动的路程为:2t=2t,
乙到原点的距离:62t(0t3)
②当t>3时,乙球从原点O处开始一直向右运动,
此时乙球到原点的距离为:2t6(t>3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把下列各数分别填在相应的集合里:
-2.4,3,![]() ,
,![]() ,0.333…,-(2.28),3.14,
,0.333…,-(2.28),3.14,![]() ,1.010010001…(相邻两个1之间0的个数增加1),
,1.010010001…(相邻两个1之间0的个数增加1),![]() .
.
(1)正有理数集合{ ……}
(2)整数集合{ ……}
(3)负分数集合{ ……}
(4)无理数集合{ ……}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时, ![]() ?
? ![]() 当x取什么值时,y的值随x的增大而减小?
当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能很快算出![]() 吗?
吗?
为了解决这个问题,我们考察个位上的数为5的正整数的平方,任意一个个位数为5的正整数可写成10n+5(n为正整数),即求![]() 的值,试分析
的值,试分析![]() ,2,3……这些简单情形,从中探索其规律.
,2,3……这些简单情形,从中探索其规律.
⑴通过计算,探索规律:
![]() 可写成
可写成![]() ;
;
![]() 可写成
可写成![]() ;
;
![]() 可写成
可写成![]() ;
;
![]() 可写成
可写成![]() ;………………
;………………
![]() 可写成________________________________
可写成________________________________
![]() 可写成________________________________
可写成________________________________
⑵根据以上规律,试计算![]() =
=
![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
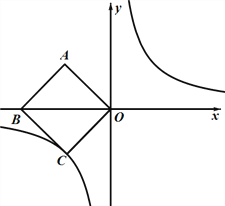
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】彩虹服装店用![]() 元购进
元购进![]() 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件![]() 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元).他卖完这
(单位:元).他卖完这![]() 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF的内角都相等, ![]() ,则下列结论成立的个数是
,则下列结论成立的个数是![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() 四边形ACDF是平行四边形;
四边形ACDF是平行四边形; ![]() 六边形ABCDEF既是中心对称图形,又是轴对称图形.
六边形ABCDEF既是中心对称图形,又是轴对称图形.
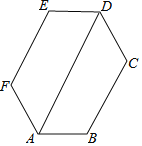
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
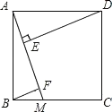
【题目】如图,正方形 ABCD 的边长为 5,点 M 是边 BC 上的点,DE⊥AM 于点 E,BF∥DE,交 AM 于点 F.若E 是 AF 的中点,则 DE 的长为( )
A.![]() B.2
B.2![]() C.4D.
C.4D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com