
【题目】如图,六边形ABCDEF的内角都相等, ![]() ,则下列结论成立的个数是
,则下列结论成立的个数是![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() 四边形ACDF是平行四边形;
四边形ACDF是平行四边形; ![]() 六边形ABCDEF既是中心对称图形,又是轴对称图形.
六边形ABCDEF既是中心对称图形,又是轴对称图形.
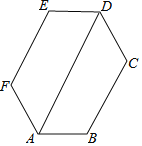
A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】试题解析:∵六边形ABCDEF的内角都相等,
![]()
![]()
![]()
![]()
∴AD![]() EF
EF![]() CB,故②正确,
CB,故②正确,
![]()
![]()
∴∠EDA=∠DAB,
∴AB![]() DE,故①正确,
DE,故①正确,
∵∠FAD=∠EDA,∠CDA=∠BAD,EF![]() AD
AD![]() BC,
BC,
∴四边形EFAD,四边形BCDA是等腰梯形,
∴AF=DE,AB=CD,
∵AB=DE,
∴AF=CD,故③正确,
连接CF与AD交于点O,连接DF、AC、AE、DB、BE.
∵∠CDA=∠DAF,
∴AF![]() CD,AF=CD,
CD,AF=CD,
∴四边形AFDC是平行四边形,故④正确,
同法可证四边形AEDB是平行四边形,
∴AD与CF,AD与BE互相平分,
∴OF=OC,OE=OB,OA=OD,
∴六边形ABCDEF既是中心对称图形,故⑤正确,
故选D.



科目:初中数学 来源: 题型:
【题目】数轴上从左到右的三个点![]() ,
,![]() ,
,![]() 所对应的数分别为
所对应的数分别为![]() ,
,![]() ,
,![]() .其中
.其中![]() ,
,![]() ,如图所示.
,如图所示.
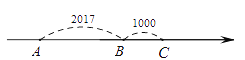
(1)若以![]() 为原点,写出点
为原点,写出点![]() ,
,![]() 所对应的数,并计算
所对应的数,并计算![]() 的值.
的值.
(2)若原点![]() 在
在![]() ,
,![]() 两点之间,求
两点之间,求![]() 的值.
的值.
(3)若![]() 是原点,且
是原点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,且a、b满足|a+2|+(b6)2=0![]()
(1)点A表示的数为 ;点B表示的数为 ;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=3BC,则C点表示的数 ;
(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请分别表示出甲、乙两小球到原点的距离(用t表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(1)求k,a,b的值;
(2)直线x=m与![]() (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.
求证DE=AF.

证法1:∵DE是△ABC的中位线,
∴DE= .
∵AF是△ABC的中线,∠BAC=90°,
∴AF= ,
∴DE=AF.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的几个算式:
1+2+1=4=2×2;1+2+3+2+1=9=3×3;
1+2+3+4+3+2+1=16=4×4;![]() 。
。
根据上面几道题的规律,计算下面的题:
1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1的值为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各数填在相应的集合内,注意数与数要用逗号隔开
![]() ,
,![]() ,0 ,
,0 ,![]() ,8 ,-2 ,25% ,-3.8 ,0.1011 ,100 ,-200
,8 ,-2 ,25% ,-3.8 ,0.1011 ,100 ,-200
负数集合:{ …};
整数集合:{ … };
非负集合:{ … };
分数集合:{ … };
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动 5 个单位长度,可以看到终点表示的数是![]() .已知点
.已知点![]() 、
、![]() 是数轴上的点,完成下列各题:
是数轴上的点,完成下列各题:
![]()
(1)如果点![]() 表示数- 3,将点
表示数- 3,将点![]() 向右移动 7 个单位长度,那么终点
向右移动 7 个单位长度,那么终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、![]() 两点间的距离是 .
两点间的距离是 .
(2)如果点![]() 表示数是3,将点
表示数是3,将点![]() 向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点
向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、 ![]() 两点间的距离是 .
两点间的距离是 .
(3)一般地,如果点![]() 表示数为
表示数为![]() ,将点
,将点![]() 向右移动
向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,那么请你猜想终点
个单位长度,那么请你猜想终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、![]() 两点间的距离是 .
两点间的距离是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com