【题目】下列各数填在相应的集合内，注意数与数要用逗号隔开
，
，0 ，
，8 ，－2 ，25% ，－3.8 ，0.1011 ，100 ，－200
负数集合：｛ …｝；
整数集合：｛ … ｝；
非负集合：｛ … ｝；
分数集合：｛ … ｝；
【答案】
， 
， －2 ，－3.8， －200；0, 8， -2, 100， -200；
， 0， 8， 25%， 0.1011， 100；， ， ， 25%， －3.8， 0.1011.
负数集合：｛ ， ， －2 ，－3.8，－200 …｝；
整数集合：｛0, 8， -2, 100， -200 … ｝；
非负集合：｛， 0， 8， 25%， 0.1011， 100 … ｝；
分数集合：｛， ， ， 25%，－3.8， 0.1011， … ｝；
【解析】
利用负数，整数，分数，以及非负数定义判断即可．
负数：比0小的数叫负数；
非负数：正数和零的总称.；
分数：分数是一个整数a和一个正整数b的不等于整数的比.
负数集合：｛ ， ， －2 ，－3.8，－200 …｝；
整数集合：｛0, 8， -2, 100， -200 … ｝；
非负集合：｛， 0， 8， 25%， 0.1011， 100 … ｝；
分数集合：｛， ， ， 25%，－3.8， 0.1011， … ｝；
新非凡教辅冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】你能很快算出
吗？
为了解决这个问题，我们考察个位上的数为5的正整数的平方，任意一个个位数为5的正整数可写成10n＋5（n为正整数），即求
的值，试分析
，2，3……这些简单情形，从中探索其规律.
⑴通过计算，探索规律:
可写成
；
可写成
；
可写成
；
可写成
；………………
可写成________________________________
可写成________________________________
⑵根据以上规律，试计算
=
=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，六边形ABCDEF的内角都相等， 
，则下列结论成立的个数是
； 
； 
； 
四边形ACDF是平行四边形； 
六边形ABCDEF既是中心对称图形，又是轴对称图形．
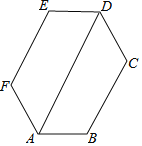
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，ABCD的周长为22m，对角线AC、BD交于点O，过点O与AC垂直的直线交边AD于点E，则△CDE的周长为（ ）
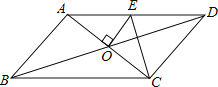
A. 8cmB. 9cmC. 10cmD. 11cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动5个单位长度，可以看到终点表示的数是-2，已知点A，B是数轴上的点，请参照图并思考，完成下列各题．
(1)如果点A表示数-3，将点A向右移动7个单位长度，那么终点B表示的数是_____，A，B两点间的距离是_____；
(2)如果点A表示数3，将A点向左移动7个单位长度，再向右移动5个单位长度，那么终点表示的数是_____，A，B两点间的距离为_____；
(3)如果点A表示数-4，将A点向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是_____，A、B两点间的距离是_____；
(4)一般地，如果A点表示的数为m，将A点向右移动n个单位长度，再向左移动p个单位长度，那么请你猜想终点B表示什么数？A，B两点间的距离为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某一中学位于东西方向的一条路上，一天我们学校的李老师出校门去家访，他先向东走100米到聪聪家,再向西走150米到青青家,再向东走200米到刚刚家,请问:
【1】聪聪家与刚刚家相距多远?
【2】如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出他们家与学校的大概位置(数轴上50米表示单位1).
【3】聪聪家向西210米所表示的数是多少?
【4】你认为可用什么办法求数轴上两点之间的距离?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形 ABCD 的边长为 5，点 M 是边 BC 上的点，DE⊥AM 于点 E，BF∥DE，交 AM 于点 F．若E 是 AF 的中点，则 DE 的长为（ ）
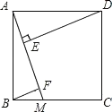
A.
B.2C.4D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c，其中AB=BC.如果
，那么该数轴的原点O的位置应该在（ ）
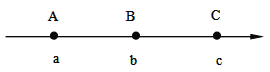
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
查看答案和解析>>
科目：初中数学 来源： 题型：
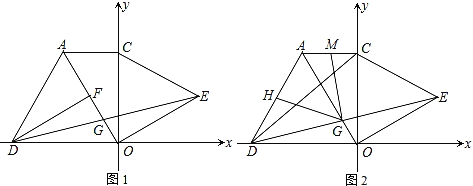
【题目】如图，在平面直角坐标系中，∠ACO＝90°，∠AOC＝30°，分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE，DF⊥AO于F，连DE交AO于G．
（1）求证：△DFG≌△EOG；
（2）H为AD的中点，连HG，求证：CD＝2HG；
（3）在（2）的条件下，AC＝4，若M为AC的中点，求MG的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com