
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于 ![]() 两点,与
两点,与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,其顶点为
,其顶点为![]() .
.
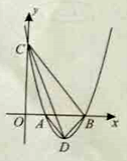
(1)写出![]() 两点的坐标(用含
两点的坐标(用含![]() 的式子表示);
的式子表示);
(2)设![]() ,求
,求![]() 的值;
的值;
(3)当![]() 是直角三角形时,求对应抛物线的解析式.
是直角三角形时,求对应抛物线的解析式.
【答案】(1)C(0,3a),D(2,﹣a);(2)3;(3)y=x2﹣4x+3或y=![]() x2﹣2
x2﹣2![]() x+
x+![]() .
.
【解析】
试题分析:(1)令x=0可求得C点坐标,化为顶点式可求得D点坐标;
(2)令y=0可求得A、B的坐标,结合D点坐标可求得△ABD的面积,设直线CD交x轴于点E,由C、D坐标,利用待定系数法可求得直线CD的解析式,则可求得E点坐标,从而可表示出△BCD的面积,可求得k的值;
(3)由B、C、D的坐标,可表示出BC2、BD2和CD2,分∠CBD=90°和∠CDB=90°两种情况,分别利用勾股定理可得到关于a的方程,可求得a的值,则可求得抛物线的解析式.
试题解析:(1)在y=a(x﹣1)(x﹣3),令x=0可得y=3a,
∴C(0,3a),
∵y=a(x﹣1)(x﹣3)=a(x2﹣4x+3)=a(x﹣2)2﹣a,
∴D(2,﹣a);
(2)在y=a(x﹣1)(x﹣3)中,令y=0可解得x=1或x=3,
∴A(1,0),B(3,0),
∴AB=3﹣1=2,
∴S△ABD=![]() ×2×a=a,
×2×a=a,
如图,设直线CD交x轴于点E,设直线CD解析式为y=kx+b,

把C、D的坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线CD解析式为y=﹣2ax+3a,令y=0可解得x=![]() ,
,
∴E(![]() ,0),
,0),
∴BE=3﹣![]() =
=![]()
∴S△BCD=S△BEC+S△BED=![]() ×
×![]() ×(3a+a)=3a,
×(3a+a)=3a,
∴S△BCD:S△ABD=(3a):a=3,
∴k=3;
(3)∵B(3,0),C(0,3a),D(2,﹣a),
∴BC2=32+(3a)2=9+9a2,CD2=22+(﹣a﹣3a)2=4+16a2,BD2=(3﹣2)2+a2=1+a2,
∵∠BCD<∠BCO<90°,
∴△BCD为直角三角形时,只能有∠CBD=90°或∠CDB=90°两种情况,
①当∠CBD=90°时,则有BC2+BD2=CD2,即9+9a2+1+a2=4+16a2,解得a=﹣1(舍去)或a=1,此时抛物线解析式为y=x2﹣4x+3;
②当∠CDB=90°时,则有CD2+BD2=BC2,即4+16a2+1+a2=9+9a2,解得a=﹣![]() (舍去)或a=
(舍去)或a=![]() ,此时抛物线解析式为y=
,此时抛物线解析式为y=![]() x2﹣2
x2﹣2![]() x+
x+![]() ;
;
综上可知当△BCD是直角三角形时,抛物线的解析式为y=x2﹣4x+3或y=![]() x2﹣2
x2﹣2![]() x+
x+![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,适合采用全面调查(普查)方式的是( )
A.了解湖南卫视的收视率
B.了解湘江中草鱼种群数量
C.了解全国快递包裹产生包装垃圾的数量
D.了解某班同学“跳绳”的成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: 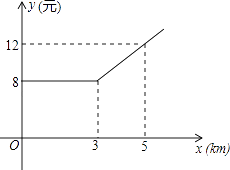
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b = ab2 + a.如:1☆3=1×32+1=10. 则(-2)☆3的值为( )
A.10B.-15C.-16D.-20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=6cm,BC=4cm,则AC的取值范围是( )
A. AC≥2cm B. AC≤10cm C. 2cm≤AC≤10cm D. 无法判定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘西土家族苗族自治州6月2日至6月8日最高气温(℃)统计如下表:
日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 |
最高气温℃ | 28 | 25 | 25 | 30 | 32 | 28 | 27 |
则这七天最高气温的中位数为( )
A.25℃
B.27℃
C.28℃
D.30℃
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com