练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

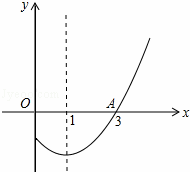
    如图，是二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是　　．


    ﹣1＜x＜3

                  解：由图象得：对称轴是x=1，其中一个点的坐标为（3，0）

    ∴图象与x轴的另一个交点坐标为（﹣1，0）

    利用图象可知：

    ax2+bx+c＜0的解集即是y＜0的解集，

    ∴﹣1＜x＜3


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3=　　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（　　）

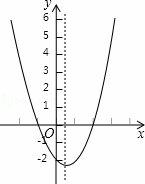
    A．  函数有最小值  B．  对称轴是直线x=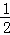   C．    当x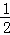＜，y随x的增大而减小    D． 当﹣1＜x＜2时，y＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1．

    ①b2＞4ac；        

    ②4a﹣2b+c＜0；

    ③不等式ax2+bx+c＞0的解集是x≥3.5；

    ④若（﹣2，y1），（5，y2）是抛物线上的两点，则y1＜y2．

    上述4个判断中，正确的是（　　）

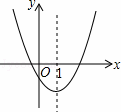
    A．  ①②          B．①④          C．①③④        D． ②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果将抛物线y=x2向右平移1个单位，那么所得的抛物线的表达式是（　　）

    A．  y=x2﹣1       B．y=x2+1        C．y=（x﹣1）2   D． y=（x+1）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


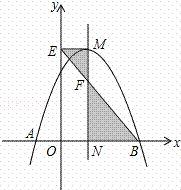
    如图，抛物线y=﹣x2+2x+c与x轴交于A，B两点，它的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F，已知点A的坐标为（﹣1，0）．

    （1）求该抛物线的解析式及顶点M的坐标．

    （2）求△EMF与△BNF的面积之比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2）．把一条长为2014个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（　　）

    A．  （﹣1，0）    B．（1，﹣2）    C．（1，1）      D． （﹣1，﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


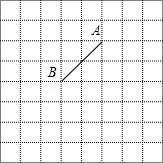
    请在所给网格中按下列要求操作：

    （1）请在网格中建立平面直角坐标系，使A点坐标为（0，2），B点坐标为（﹣2，0）；

    （2）在x轴上画点C，使△ABC为等腰三角形，请画出所有符合条件的点C，并直接写出相应的C点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    函数y=+中自变量x的取值范围是　

    查看答案和解析>>

    同步练习册答案