
| A. | $\frac{c}{a+b}$ | B. | $\frac{b}{a+b+c}$ | C. | $\frac{a+c}{a+b+c}$ | D. | $\frac{a+c}{b}$ |
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,AB=AC=6,∠A=45°,点D在AC上,点E在BD上,且△ABD、△CDE、△BCE均为等腰三角形.
已知:如图,△ABC中,AB=AC=6,∠A=45°,点D在AC上,点E在BD上,且△ABD、△CDE、△BCE均为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC与BD交于O点,∠1=∠2,下列不能使△ABO≌△DCO的条件是( )
如图,AC与BD交于O点,∠1=∠2,下列不能使△ABO≌△DCO的条件是( )| A. | ∠A=∠D | B. | AC=BD | C. | AB=DC | D. | ∠ABC=∠DCB |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、
如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、查看答案和解析>>
科目:初中数学 来源: 题型:选择题
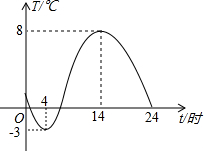 如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-3℃ | |
| B. | 从0时至14时,气温随时间增长而上升 | |
| C. | 14时气温最高为8℃ | |
| D. | 从14时至24时,气温随时间增长而下降 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com