
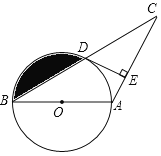
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若⊙O的半径为3cm,∠C=30°,求图中阴影部分的面积.
【答案】(1)见解析;(2)(3π﹣![]() )cm2
)cm2
【解析】
(1)由等腰三角形的性质证出∠ODB=∠C.得出OD∥AC.由已知条件证出DE⊥OD,即可得出结论;
(2)由垂径定理求出OF,由勾股定理得出DF,求出BD,得出△BOD的面积,再求出扇形BOD的面积,即可得出结果.
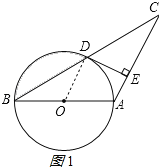
(1)连接OD,如图1所示:
∵OD=OB,
∴∠B=∠ODB.
∵AB=AC,
∴∠B=∠C.
∴∠ODB=∠C.
∴OD∥AC.
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线.
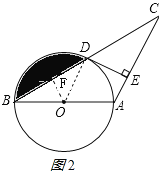
(2)过O作OF⊥BD于F,如图2所示:
∵∠C=30°,AB=AC,OB=OD,
∴∠OBD=∠ODB=∠C=30°,
∴∠BOD=120°,
在Rt△DFO中,∠FDO=30°,
∴OF=![]() OD=
OD=![]() cm,
cm,
∴DF=![]() =
=![]() cm,
cm,
∴BD=2DF=3![]() cm,
cm,
∴S△BOD=![]() ×BD×OF=
×BD×OF=![]() ×3
×3![]() ×
×![]() =
=![]() cm2,
cm2,
S扇形BOD=![]() =3πcm2,
=3πcm2,
∴S阴=S扇形BOD﹣S△BOD==(3π﹣![]() )cm2.
)cm2.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04).

A.12.1mB.13.3m
C.16.9mD.18.1m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图所示,某地区对某种药品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x + 70,y2=2x-38,需求量为0时,即停止供应.当y1=y2时,该药品的价格称为稳定价格,需求量称为稳定需求量.
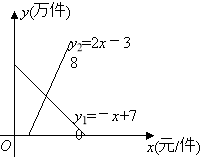
(1)求该药品的稳定价格与稳定需求量.
(2)价格在什么范围内,该药品的需求量低于供应量?
(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加6万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.
查看答案和解析>>
科目:初中数学 来源: 题型:
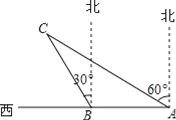
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
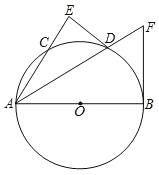
【题目】如图,AB是直经,D是![]() 的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
(1)求证:DE是⊙O的切线.
(2)试探究AE,AD,AB三者之间的等量关系.
(3)若DE=3,⊙O的半径为5,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
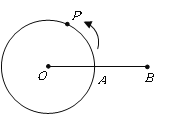
【题目】如图,![]() 是半径为
是半径为![]() 的
的![]() 上的定点,动点
上的定点,动点![]() 从
从![]() 出发,以
出发,以![]() 的速度沿圆周逆时针运动,当点
的速度沿圆周逆时针运动,当点![]() 回到
回到![]() 地立即停止运动.
地立即停止运动.
(1)如果![]() ,求点
,求点![]() 运动的时间;
运动的时间;
(2)如果点![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() ,那么当点
,那么当点![]() 运动的时间为
运动的时间为![]() 时,判断直线
时,判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
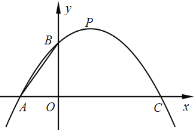
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com