
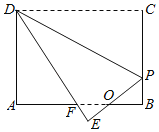
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则BF的长为_____.
【答案】![]()
【解析】
根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP,根据全等三角形的性质可得出OE=OB、EF=BP,设BF=EP=CP=x,则AF=4﹣x,BP=3﹣x=EF,DF=DE﹣EF=4﹣(3﹣x)=x+1,依据Rt△ADF中,AF2+AD2=DF2,即可得到x的值.
解:根据折叠可知,DC=DE=4,CP=EP,∠B=∠E=90°,
在△OEF和△OBP中,
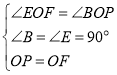 ,
,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP,
∴BF=EP=CP,
设BF=EP=CP=x,则AF=4﹣x,BP=3﹣x=EF,DF=DE﹣EF=4﹣(3﹣x)=x+1,
∵∠A=90°,
∴在Rt△ADF中,AF2+AD2=DF2,
即(4﹣x)2+32=(1+x)2,
解得:x=![]() ,
,
∴BF=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下面是小明主设计的“作一个含30°角的直角三角形”的尺规作图过程.
已知:直线l.
![]()
求作:△ABC,使得∠ACB=90°,∠ABC=30°.
作法:如图,
![]()
①在直线l上任取两点O,A;
②以点O为圆心,OA长为半径画弧,交直线l于点B;
③以点A为圆心,AO长为半径画弧,交![]() 于点C;
于点C;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:在⊙O中,AB为直径,
∴∠ACB=90°(① ),(填推理的依据)
连接OC
∵OA=OC=AC,
∴∠CAB=60°,
∴∠ABC=30°(② ),(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”
译文:“假设有甲乙二人,不知其钱包里有多少钱.若乙把自己一半的钱给甲,则甲的钱数为50;而甲把自己![]() 的钱给乙,则乙的钱数也能为50.问甲、乙各有多少钱?”
的钱给乙,则乙的钱数也能为50.问甲、乙各有多少钱?”
设甲持钱为x,乙持钱为y,可列方程组为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
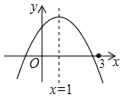
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
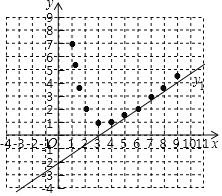
【题目】在平面直角坐标系xOy中,函数y1=![]() x﹣2的图象与函数y2=
x﹣2的图象与函数y2=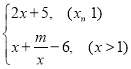 的图象在第一象限有一个交点A,且点A的横坐标是6.
的图象在第一象限有一个交点A,且点A的横坐标是6.
(1)求m的值;
(2)补全表格并以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,补充画出y2的函数图象;
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 1.2 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y2 | ﹣1 | 1 | 5 | 7 | 5.2 | 3.5 | 2 | 1 | 1 | 2 |
|
|
|
(3)写出函数y2的一条性质: ;
(4)已知函数y1与y2的图象在第一象限有且只有一个交点A,若函数y3=![]() x+n与y2的函数图象有三个交点,求n的取值范围.
x+n与y2的函数图象有三个交点,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
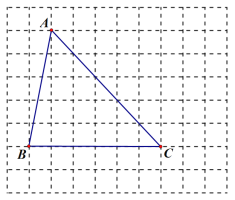
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中,△ABC的顶点都在网格线交点上.
(1)图中AC边上的高为 个单位长度;
(2)只用没有刻度的直尺,在所给网格图中按如下要求画图(保留必要痕迹):
①以点C为位似中心,把△ABC按相似比1:2缩小,得到△DEC;
②以AB为一边,作矩形ABMN,使得它的面积恰好为△ABC的面积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
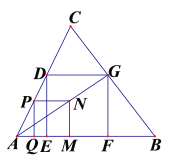
【题目】如图,正方形PQMN在△ABC内,点P在AC上,点Q、M在AB上,N在△ABC内,连接AN并延长交BC于G,过G点作GD∥AB交AC于D,过D、G分别作DE ⊥AB,GF⊥AB,垂足分别为E、F.
(1)求证:DG=GF;
(2)若AB=10,S△ABC=40,试求四边形DEFG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com