
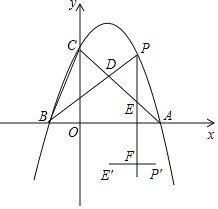
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是直线AC上方的抛物线上一动点(异于点A、C),连接BC,AC,PA,PB,PB与AC交于点D,设点P的横坐标为m.
①若△CBD,△DAP的面积分别为S1和S2,当S1﹣S2最小时,求点P的坐标;
②过点P作x轴的垂线,交AC于点E.以原点O为旋转中心,将线段PE顺时针旋转90°,得到线段P′E′.当线段P′E′与直线PE有交点时,设交点为F,求交点F的路径长.
【答案】(1)y=﹣x2+2x+3;(2)①P(1,4);②![]() .
.
【解析】
(1)设抛物线的表达式为:y=a(x﹣3)(x+1),利用待定系数法求二次函数解析式解答即可;
(2)①求直线AC的解析式,然后分别表示出![]() 两个三角形的面积,然后求S1﹣S2的解析式,从而求最小值,最后确定点P坐标;
两个三角形的面积,然后求S1﹣S2的解析式,从而求最小值,最后确定点P坐标;
②根据旋转的性质求线段P′E′与直线PE有交点时,m的取值范围,从而求解.
解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0)
∴设抛物线的表达式为:y=a(x﹣3)(x+1)=a(x2﹣2x﹣3),
将(0,3)代入得,﹣3a=3,解得:a=﹣1,
∴抛物线的表达式为:y=﹣x2+2x+3;
(2)设![]() ,将点A(3,0)、C(0,3)的坐标代入一次函数表达式得:
,将点A(3,0)、C(0,3)的坐标代入一次函数表达式得:![]() ,解得
,解得![]()
∴直线AC的表达式为:y=﹣x+3,
设点P(m,﹣m2+2m+3),则点E(m,﹣m+3),
①S1﹣S2=S△BAC﹣S△BAP=![]() ×AB×(3+m2﹣2m﹣3)=2(m2﹣2m)=
×AB×(3+m2﹣2m﹣3)=2(m2﹣2m)=![]() ,
,
∴当m=1时,S1﹣S2最小,此时点P(1,4);
②将线段PE顺时针旋转90°,得到线段P′E′,
则点E′、P′的坐标分别为:(﹣m+3,﹣m)、(﹣m2+2m+3,﹣m),
当线段P′E′与直线PE有交点时,即点F在E′P′之间,
即﹣m+3≤m≤﹣m2+2m+3,
解得:![]() ≤m≤
≤m≤![]() ,
,
故交点F的路径长为:![]() ﹣
﹣![]() =
=![]() .
.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)求抛物线的对称轴;
(2)当![]() 时,设抛物线与
时,设抛物线与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),顶点为
左侧),顶点为![]() ,若
,若![]() 为等边三角形,求
为等边三角形,求![]() 的值;
的值;
(3)过![]() (其中
(其中![]() )且垂直
)且垂直![]() 轴的直线
轴的直线![]() 与抛物线交于
与抛物线交于![]() 两点.若对于满足条件的任意
两点.若对于满足条件的任意![]() 值,线段
值,线段![]() 的长都不小于1,结合函数图象,直接写出
的长都不小于1,结合函数图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,5),B(0,0),C(4,0),D(2019,m),E(2020,n)在某二次函数的图象上.下列结论:①图象开口向上;②图象的对称轴是直线x=2;③m<n;④当0<x<4时,y<0.其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
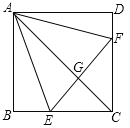
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:
①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
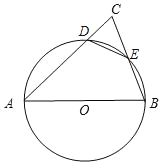
【题目】如图,AB为⊙O的直径,△ABC的边AC,BC分别与⊙O交于D,E,若E为![]() 的中点.
的中点.
(1)求证:DE=EC;
(2)若DC=2,BC=6,求⊙O的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() +b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
+b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量x的取值范围;
(2)请在下列直角坐标系中画出该函数的图象;
(3)请你在上方直角坐标系中画出函数y=2x的图象,结合上述函数的图象,写出不等式![]() +b≤2x的解集.
+b≤2x的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com