
【题目】已知点A(﹣1,5),B(0,0),C(4,0),D(2019,m),E(2020,n)在某二次函数的图象上.下列结论:①图象开口向上;②图象的对称轴是直线x=2;③m<n;④当0<x<4时,y<0.其中正确的个数是( )
A.1B.2C.3D.4
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)如图1,E为线段DC上任意一点,将线段![]() 绕点D逆时针旋转90°得到线段
绕点D逆时针旋转90°得到线段![]() ,连接
,连接![]() ,过点F作
,过点F作![]() ,交直线
,交直线![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)如图2,若![]() 为线段
为线段![]() 的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.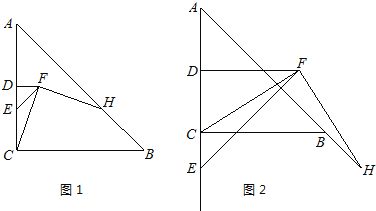
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若AC=3,BC=4,OA=1,求线段DE的长.
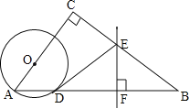
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸飞机是我们儿时快乐的回忆,现有一张长为290mm,宽为200mm的白纸,如图所示,以下面几个步骤折出纸飞机:(说明:第一步:白纸沿着EF折叠,AB边的对应边A′B′与边CD平行,将它们的距离记为x;第二步:将EM,MF分别沿着MH,MG折叠,使EM与MF重合,从而获得边HG与A′B′的距离也为x),则PD=______mm.
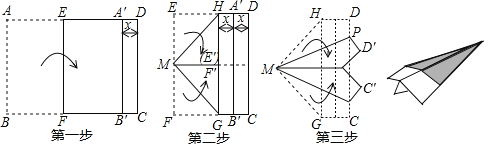
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解方程:
(1)用配方法解6x2+x﹣2=0;
(2)在解方程x2﹣2x=2﹣x时,某同学的解答如下,请你指出解答中出现的错误,并给出正确解题过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是直线AC上方的抛物线上一动点(异于点A、C),连接BC,AC,PA,PB,PB与AC交于点D,设点P的横坐标为m.
①若△CBD,△DAP的面积分别为S1和S2,当S1﹣S2最小时,求点P的坐标;
②过点P作x轴的垂线,交AC于点E.以原点O为旋转中心,将线段PE顺时针旋转90°,得到线段P′E′.当线段P′E′与直线PE有交点时,设交点为F,求交点F的路径长.
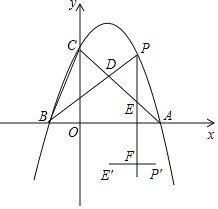
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求此抛物线的解析式;
(2)已知点D![]() 在第四象限的抛物线上,求点D关于直线BC对称的点D’的坐标;
在第四象限的抛物线上,求点D关于直线BC对称的点D’的坐标;
(3)在(2)的条件下,连结BD,问在x轴上是否存在点P,使![]() ,若存在,请求出P点的坐标;若不存在,请说明理由.
,若存在,请求出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象经过A,B,C三点,点C在y轴正半轴上,已知A(﹣1,0),B(3,0),OC=AB.
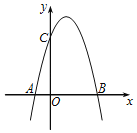
(1)求点C的坐标.
(2)求二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com