
【题目】已知点A(0,4),B(4,0),C(10,0),点P在直线AB上,且∠OPC=90,则点P的坐标为________________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0).
(1)求此二次函数的表达式;
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣![]() ,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
(3)如图2,点M在抛物线上,且点M的横坐标是1,将射线MA绕点M逆时针旋转45°,交抛物线于点P,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今,网上购物已成为一种消费常态,纪念日饰品店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网店(如图所示),已知两家网店的贺年卡质量相同,请看图回答下列问题:
甲 网 店 | 鼎发贺年卡 ¥1.00 产地:杭州 如实描述 信守天下 运费:8.00 七天退换 超过30个全部按六折 信用卡 最近售出11619个 |
乙 网 店 | 鼎发贺年卡 ¥0.80 产地:杭州 如实描述 信守天下 运费:8.00 七天退换 超过30个免运费 信用卡 最近售出10137个 |
(1)假如纪念日饰品店想购买x个贺年卡,那么在甲、乙两家网店分别需要花多少钱(用含x的式子表示)?(提示:如需付运费时,运费只需付一次,即8元)
(2)纪念日饰品店打算购买300个贺年卡,它应选择哪家网店省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=![]() +
+![]() -1.
-1.
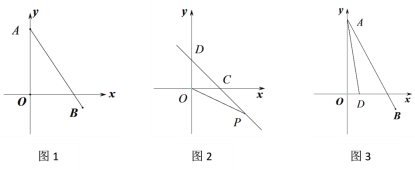
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
(1)求证:四边形BDFC是平行四边形;
(2)若CB=CD,求四边形BDFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第二次将点A向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是( )
![]()
A. 12B. 13C. 14D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
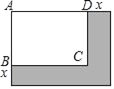
【题目】如图,矩形ABCD的长BC=5,宽AB=3.
(1)若矩形的长与宽同时增加2,则矩形的面积增加 .
(2)若矩形的长与宽同时增加x,此时矩形增加的面积为48,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
(1)如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;
(2)如图①,若∠BOC=10°,求∠AOD的度数;
(3)如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;
(4)若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com