
【题目】如图,已知∠1+∠2=180°,∠DAE=∠BCF.
(1)试判断直线AE与CF有怎样的位置关系?并说明理由;
(2)若∠BCF=70°,求∠ADF的度数.
【答案】
(1)解:AE∥CF,
理由是:∵∠1+∠2=180°,∠BDC+∠2=180°,
∴∠1=∠BDC,
∴AE∥CF;
(2)解:∵AE∥CF,
∴∠BCF=∠CBE,
又∵∠DAE=∠BCF,
∴∠DAE=∠CBE,
∴AD∥BC,
∴∠ADF=∠BCF=70°.
【解析】(1)根据图形可知∠BDC+∠2=180°或∠DBC+∠1=180°,结合已知,根据同角的余角相等,得出∠1=∠BDC或∠DBC=∠2证得结论。
(2)先根据已知证明∠DAE=∠CBE,再根据平行线的判定得出AD∥BC,然后根据两直线平行同位角相等,即可求出结果。
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.


科目:初中数学 来源: 题型:
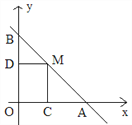
【题目】如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D。
(1)当点M在AB上运动时,四边形OCMD的周长为________;
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0<a≤4),在平移过程中:
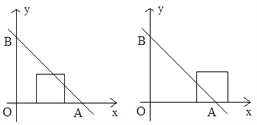
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________;
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
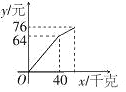
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造![]() 个新公共自行车站点和配置
个新公共自行车站点和配置![]() 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com