
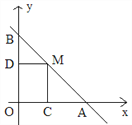
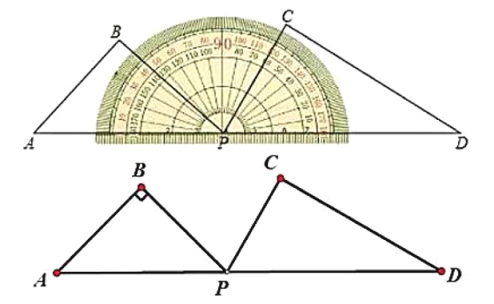
ЁОЬтФПЁПШчЭМЃЌжБЯпy=4ЃxгыСНзјБъжсЗжБ№ЯрНЛгкAЁЂBЕуЃЌЕуMЪЧЯпЖЮABЩЯШЮвтвЛЕу(AЁЂBСНЕуГ§Эт)ЃЌЙ§MЗжБ№зїMCЁЭOAгкЕуCЃЌMDЁЭOBгкЕуDЁЃ
(1)ЕБЕуMдкABЩЯдЫЖЏЪБЃЌЫФБпаЮOCMDЕФжмГЄЮЊ________ЃЛ
(2)ЕБЫФБпаЮOCMDЮЊе§ЗНаЮЪБЃЌНЋе§ЗНаЮOCMDбизХxжсЕФе§ЗНЯђвЦЖЏЃЌЩшЦНвЦЕФОрРыЮЊa (0<aЁм4)ЃЌдкЦНвЦЙ§ГЬжаЃК
ЂйЕБЦНвЦОрРыa=1ЪБ, е§ЗНаЮOCMDгыЁїAOBжиЕўВПЗжЕФУцЛ§ЮЊ________ЃЛ
ЂкЕБЦНвЦОрРыaЪЧЖрЩйЪБЃЌе§ЗНаЮOCMDЕФУцЛ§БЛжБЯпABЗжГЩlЃК3СНИіВПЗж?
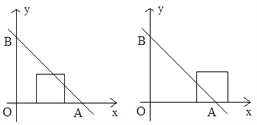
ЁОД№АИЁПЃЈ1ЃЉ8ЃЛЃЈ2ЃЉЂй3.5ЃЛЂкa=![]() Лђ
Лђ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшЕуMЕФКсзјБъЮЊxЃЌдђЕуMЕФзнзјБъЮЊ-x+4ЃЈ0ЃМxЃМ4ЃЌxЃО0ЃЌ-x+4ЃО0ЃЉИљОнЫФБпаЮЕФжмГЄМЦЫуЗНЗЈМЦЫуМДПЩЗЂЯжЃЌЕБЕуMдкABЩЯдЫЖЏЪБЃЌЫФБпаЮOCMDЕФжмГЄВЛЗЂЩњБфЛЏЃЌзмЪЧЕШгк8ЃЎ
ЃЈ2ЃЉЂйЕБ0ЃМaЁм2ЪБЃЌS=4-![]() a2=-
a2=-![]() a2+4,ВЂЧвa=1ПЩЧѓГіжиЕўВПЗжЕФУцЛ§ЃЛ
a2+4,ВЂЧвa=1ПЩЧѓГіжиЕўВПЗжЕФУцЛ§ЃЛ
ЂкЕБЫФБпаЮЮЊOCMDЮЊе§ЗНаЮЪБЃЌЯШЧѓЕУе§ЗНаЮЕФБпГЄЃЌДгЖјПЩЧѓЕУе§ЗНаЮЕФУцЛ§ЃЌПЩЧѓЕУе§ЗНаЮБЛжБЯпЗжГЩЕФНЯаЁЕФВПЗжЕФУцЛ§ЮЊ1ЃЌШЛКѓдйжЄУїЁАНЯаЁЕФВПЗжЁБЮЊЕШбќжБНЧШ§НЧаЮЃЌДгЖјПЩЧѓЕУИУЕШбќжБНЧШ§НЧаЮЕФжБНЧБпЕФГЄЖШЃЌгкЪЧПЩЧѓЕУЦНвЦЕФОрРыЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЃЈ1ЃЉЩшOC=xЃЌдђCM=4-xЃЎ
ЁпMCЁЭOAЃЌMDЁЭOBЃЌODЁЭOCЃЌ
ЁрЫФБпаЮOCMDЮЊОиаЮЃЌ
ЁрЫФБпаЮOCMDЕФжмГЄ=OD+OC+CM+DM=2ЃЈCO+CMЃЉ=2ЃЈx+4-xЃЉ=2ЁС4=8ЃЎ
ЃЈ2ЃЉЂйШчЭМЃЈ 2 ЃЉЃЌЕБ0ЃМaЁм2ЪБЃЌS=SЫФБпаЮOЁфCMD-SЁїMEF=4-![]() a2=-
a2=-![]() a2+4ЃЌ
a2+4ЃЌ
ЂкЁпЕБЫФБпаЮЮЊOCMDЮЊе§ЗНаЮЪБЃЌOC=CMЃЌМДx=4-xЃЌНтЕУЃКx=2ЃЌ
ЁрSе§ЗНаЮOCMDЕФУцЛ§=4ЃЎ
Ёпе§ЗНаЮOCMDЕФУцЛ§БЛжБЯпABЗжГЩ1ЃК3СНИіВПЗжЃЌ
ЁрСНВПЗжЕФУцЛ§ЗжБ№ЮЊ1КЭ3ЃЎ
ЕБ0ЃМaЁм2ЪБЃЌШчЭМ1ЫљЪОЃК

ЁпжБЯпABЕФНтЮіЪНЮЊy=4-xЃЌ
ЁрЁЯBAO=45ЁуЃЎ
ЁрЁїMMЁфEЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЁрMMЁф=MЁфEЃЎ
Ёр![]() MMЁф2=1ЃЎ
MMЁф2=1ЃЎ
ЁрMMЁф=![]() ЃЌМДa=
ЃЌМДa=![]()
ЕБ2ЃМaЃМ4ЪБЃЌШчЭМ2ЫљЪОЃК
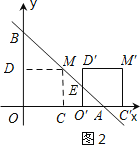
ЁпЁЯBAO=45ЁуЃЌ
ЁрЁїEOЁфAЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЁрEOЁф=OЁфAЃЎ
Ёр![]() OЁфA2=1ЃЌНтЕУЃКOЁфA=
OЁфA2=1ЃЌНтЕУЃКOЁфA=![]() ЃЎ
ЃЎ
ЁпНЋy=0ДњШыy=4-xЕУЃЛ4-x=0ЃЌНтЕУЃКx=4ЃЌ
ЁрOA=4ЃЎ
ЁрOOЁф=4-![]() ЃЌМДa=4-
ЃЌМДa=4-![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЕБЦНвЦЕФОрРыЮЊa=![]() Лђa=4
Лђa=4![]() ЪБЃЌе§ЗНаЮOCMDЕФУцЛ§БЛжБЯпABЗжГЩ1ЃК3СНИіВПЗжЃЎ
ЪБЃЌе§ЗНаЮOCMDЕФУцЛ§БЛжБЯпABЗжГЩ1ЃК3СНИіВПЗжЃЎ


 НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЁЂBЁЂCЁЂDЮЊОиаЮЕФЫФИіЖЅЕуЃЌAB=16cmЃЌBC=6cmЃЌЖЏЕуPЁЂQЗжБ№ДгЕуAЁЂCЭЌЪБГіЗЂЃЌЕуPвд3cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЕуQвд2cm/sЕФЫйЖШЯђЕуDвЦЖЏЃЎЕБЕуPдЫЖЏЕНЕуBЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙдЫЖЏЃЎ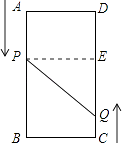
ЃЈ1ЃЉЮЪМИУыКѓЃЌЕуPКЭЕуQЕФОрРыЪЧ10cmЃП
ЃЈ2ЃЉЮЪМИУыКѓЃЌвдPЁЂQЁЂDШ§ЕуЮЊЖЅЕуЕФШ§НЧаЮЮЊжБНЧШ§НЧаЮЃП
ЃЈЬсЪОЃКИљОнВЛЭЌЧщПіЛГіВЛЭЌЕФЭМаЮЃЌдйИјгшНтОіЮЪЬтЃЎЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯпЖЮABЃН8ЃЈЕуAдкЕуBЕФзѓВрЃЉ
ЃЈ1ЃЉШєдкжБЯпABЩЯШЁвЛЕуCЃЌЪЙЕУACЃН3CBЃЌЕуDЪЧCBЕФжаЕуЃЌЧѓADЕФГЄЃЛ
ЃЈ2ЃЉШєMЪЧЯпЖЮABЕФжаЕуЃЌЕуPЪЧЯпЖЮABбгГЄЯпЩЯШЮвтвЛЕуЃЌЧыЫЕУїPA+PBЉ2PMЪЧвЛИіЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯпy=ax2+bx+cгызјБъжсЗжБ№НЛгкЕуAЃЈ0ЃЌ6ЃЉЃЌBЃЈ6ЃЌ0ЃЉЃЌCЃЈЉ2ЃЌ0ЃЉЃЌЕуPЪЧЯпЖЮABЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїPABЕФУцЛ§газюДѓжЕЃП
ЃЈ3ЃЉЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛЯпЖЮABгкЕуDЃЌдйЙ§ЕуPзіPEЁЮxжсНЛХзЮяЯпгкЕуEЃЌСЌНсDEЃЌЧыЮЪЪЧЗёДцдкЕуPЪЙЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЬзШ§НЧГпЃЈЗжБ№КЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФНЧЃЉАДШчЭМЫљЪОАкЗХдкСПНЧЦїЩЯЃЌБп
ЕФНЧЃЉАДШчЭМЫљЪОАкЗХдкСПНЧЦїЩЯЃЌБп![]() гыСПНЧЦї
гыСПНЧЦї![]() ПЬЖШЯпжиКЯЃЌБп
ПЬЖШЯпжиКЯЃЌБп![]() гыСПНЧЦї
гыСПНЧЦї![]() ПЬЖШЯпжиКЯЃЌНЋШ§НЧГп
ПЬЖШЯпжиКЯЃЌНЋШ§НЧГп![]() ШЦСПНЧЦїжааФЕу
ШЦСПНЧЦїжааФЕу![]() вдУПУы
вдУПУы![]() ЕФЫйЖШЫГЪБеыа§зЊЃЌЕББп
ЕФЫйЖШЫГЪБеыа§зЊЃЌЕББп![]() гы
гы![]() ПЬЖШЯпжиКЯЪБЭЃжЙдЫЖЏЃЌЩшШ§НЧГп
ПЬЖШЯпжиКЯЪБЭЃжЙдЫЖЏЃЌЩшШ§НЧГп![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌБп
ЪБЃЌБп![]() ОЙ§ЕФСПНЧЦїПЬЖШЯпЖдгІЕФЖШЪ§ЪЧ ЖШЃЛ
ОЙ§ЕФСПНЧЦїПЬЖШЯпЖдгІЕФЖШЪ§ЪЧ ЖШЃЛ
ЃЈ2ЃЉШєдкШ§НЧГп![]() ПЊЪМа§зЊЕФЭЌЪБЃЌШ§НЧГп
ПЊЪМа§зЊЕФЭЌЪБЃЌШ§НЧГп![]() вВШЦЕу
вВШЦЕу![]() вдУПУы
вдУПУы![]() ЕФЫйЖШФцЪБеыа§зЊЃЌЕБШ§НЧГп
ЕФЫйЖШФцЪБеыа§зЊЃЌЕБШ§НЧГп![]() ЭЃжЙа§зЊЪБЃЌШ§НЧГп
ЭЃжЙа§зЊЪБЃЌШ§НЧГп![]() вВЭЃжЙа§зЊЃЎ
вВЭЃжЙа§зЊЃЎ
ЂйЕБ![]() ЮЊКЮжЕЪБЃЌБп
ЮЊКЮжЕЪБЃЌБп![]() ЦНЗж
ЦНЗж![]() ЃЛ
ЃЛ
Ђкдка§зЊЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬЪЙ![]() ЃЌШєДцдкЃЌЧыЧѓГі
ЃЌШєДцдкЃЌЧыЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬmx2+3xЉ4=3x2гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђmЕФжЕПЩвдЪЧЃЈ ЃЉ
A.4
B.3
C.2
D.0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
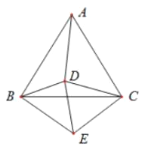
ЁОЬтФПЁПШчЭМЃЌвбжЊе§Ш§НЧаЮABCгые§Ш§НЧаЮCDEЃЌШєЁЯDBE=66ЁуЃЌдђЁЯADBЖШЪ§ЮЊ__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЈЁЊ3ЃЌЁЊ3ЃЉЃЌBЃЈЁЊ2ЃЌЁЊ1ЃЉЃЌCЃЈЁЊ1ЃЌЁЊ2ЃЉЪЧжБНЧзјБъЦНУцЩЯШ§ЕуЁЃ

ЃЈ1ЃЉЧыЛГіІЄABCЙигкдЕуOЖдГЦЕФІЄA1B1C1ЃЌ
ЃЈ2ЃЉЧыаДГіЕуBЙиЬьyжсЖдГЦЕФЕуB2ЕФзјБъЃЌШєНЋЕуB2ЯђЩЯЦНвЦhИіЕЅЮЛЃЌЪЙЦфТфдкІЄA1B1C1ФкВПЃЌжИГіhЕФШЁжЕЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯ1+ЁЯ2=180ЁуЃЌЁЯDAE=ЁЯBCFЃЎ
ЃЈ1ЃЉЪдХаЖЯжБЯпAEгыCFгадѕбљЕФЮЛжУЙиЯЕЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁЯBCF=70ЁуЃЌЧѓЁЯADFЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com