
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.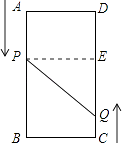
(1)问几秒后,点P和点Q的距离是10cm?
(2)问几秒后,以P、Q、D三点为顶点的三角形为直角三角形?
(提示:根据不同情况画出不同的图形,再给予解决问题.)
【答案】
(1)解:设x秒后,点P和点Q的距离是10cm,
(16﹣2x﹣3x)2+62=102,
(16﹣5x)2=64,
16﹣5x=±8,
x1=1.6,x2=4.8,
答:1.6秒或4.8秒时,点P和点Q的距离是10cm;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=16,AD=BC=6,
根据题意得:AP=3t,CQ=2t,
∴DQ=CD﹣CQ=16﹣2t,
过点Q作QM⊥AB于点M,
∴四边形BCQM是矩形,
∴QM=BC=6,BM=CQ=2t,
∴PM=AB﹣AP﹣BM=16﹣5t,
①如图1, 
若∠DPQ=90°,
∴∠APD+∠MPQ=90°,
∵∠APD=∠ADP=90°,
∴∠ADP=∠MPQ,
∵∠A=∠PMQ=90°,
∴△APD∽△MQP,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:t=2或t= ![]() ;
;
②如图2, 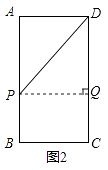
若∠DQP=90°,则有DQ2=DP2﹣PQ2,
∴(16﹣2t)2=62+(3t)2﹣62,
解得:t= ![]() ,
,
综上所述,当t=2或 ![]() 或
或 ![]() 时,△PDQ为直角三角形.
时,△PDQ为直角三角形.
【解析】(1)根据矩形的性质和勾股定理,得到一元二次方程,求出这个一元二次方程的解即可;(2)根据矩形的性质和速度得到各个边的关系式,当∠DPQ=90°时,得到△APD∽△MQP,得到比例求出t的值;当∠DQP=90°时,根据勾股定理求出t的值,在解一元二次方程时,注意实际意义.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
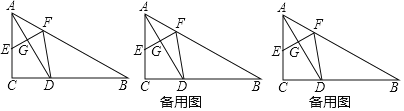
【题目】已知:如图,在△ABC中,∠C=90°,∠B=30°,AC=6,AD平分∠CAB交BC于D,E为射线AC上的一个动点,EF⊥AD交射线AB于点F,联结DF.
(1)求DB的长;
(2)当点E在线段AC上时,设AE=x,S△BDF=y,求y关于x的函数解析式;(S△BDF表示△BDF的面积)
(3)当AE为何值时,△BDF是等腰三角形.(请直接写出答案,不必写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
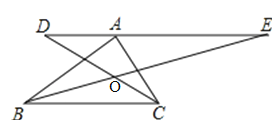
【题目】如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=_____,DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(直接开平方法)2(x+3)2﹣4=0.
(2)(配方法)y2﹣6y+6=0
(3)(公式法)2x﹣1=﹣2x2 .
(4)(因式分解法)x2﹣3x﹣28=0.
(5)x(x﹣3)+x﹣3=0.
(6)x2+x﹣12=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
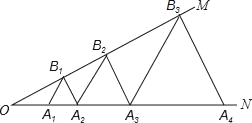
A. 32 B. 64 C. 128 D. 256
查看答案和解析>>
科目:初中数学 来源: 题型:
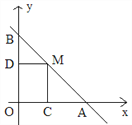
【题目】如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D。
(1)当点M在AB上运动时,四边形OCMD的周长为________;
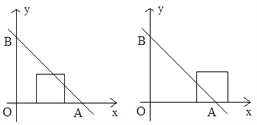
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0<a≤4),在平移过程中:
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________;
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com