
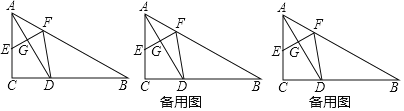
����Ŀ����֪����ͼ������ABC�У���C��90������B��30����AC��6��ADƽ�֡�CAB��BC��D��EΪ����AC�ϵ�һ�����㣬EF��AD������AB�ڵ�F������DF��
��1����DB�ij���
��2������E���߶�AC��ʱ����AE��x��S��BDF��y����y����x�ĺ�������ʽ����S��BDF��ʾ��BDF�������
��3����AEΪ��ֵʱ����BDF�ǵ��������Σ�����ֱ��д���𰸣�����д�����̣�
���𰸡���1��BC��4![]() ����2��y����
����2��y����![]() x+12
x+12![]() ��0��x��6������3����AE��ֵΪ0��12��4
��0��x��6������3����AE��ֵΪ0��12��4![]() ��12+4
��12+4![]() ʱ����BDF�ǵ��������Σ�
ʱ����BDF�ǵ��������Σ�
��������
��1�����ݺ�30�Ƚǵ�ֱ�������οɵ�AB��BC�ij�����ADƽ�֡�CAB�ɵá�CAD��![]() ��CAB��30������ֱ�������οɵ�CD�ij�����DB��BC��CD��
��CAB��30������ֱ�������οɵ�CD�ij�����DB��BC��CD��
��2����ͼ1�У���DH��AB��H�����ݽ�ƽ���ߵ����ʿɵ�DC��DH��2![]() ���ٸ�����֪ADƽ�֡�CAB��EF��AD֤����AEG����AFG����AE��AF��x��BF��12��x���������ε�������㹫ʽ���ɵ�y����x�ĺ�������ʽ��ע��x��ȡֵ��Χ��
���ٸ�����֪ADƽ�֡�CAB��EF��AD֤����AEG����AFG����AE��AF��x��BF��12��x���������ε�������㹫ʽ���ɵ�y����x�ĺ�������ʽ��ע��x��ȡֵ��Χ��
��3��������������ٵ���E��A�غ�ʱ����BDF�ǵ��������Σ��ڵ���E���߶�AC�ϣ�BD��BFʱ����BDF�ǵ��������Σ��۵���E���߶�AC���ӳ����ϣ�BF��BDʱ����BDF�ǵ��������Σ��ֱ����AE��ֵ����.
��1����Rt��ABC�У��ߡ�C��90������B��30����AC��6��
���CAB��60����AB��2AC��12��BC��![]() AC��6
AC��6![]() ��
��
��ADƽ�֡�CAB��BC��D��
���CAD��![]() ��CAB��30����
��CAB��30����
��CD��ACtan30����2![]() ��
��
��DB��BC��CD��6![]() ��2
��2![]() ��4
��4![]() ��
��
��2����ͼ1�У���DH��AB��H��
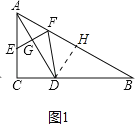
��DAƽ�֡�CAB��DC��AC��DH��AB��
��DC��DH��2![]() ��
��
��EF��AD��
���AGE����AGF��90����
�ߡ�EAG����FAG����AEG+��EAG��90������AFG+��FAG��90����
���AEG����AFG��
��AE��AF��x��
��BF��12��x��
��S��BDF��![]() BFDH��
BFDH��![]() ��12��x��2
��12��x��2![]() ����
����![]() x+12
x+12![]() ��0��x��6����
��0��x��6����
��y=��![]() x+12
x+12![]() ��0��x��6����
��0��x��6����
��3���ٵ���E��A�غ�ʱ����BDF�ǵ��������Σ���ʱx��0����AE��0��
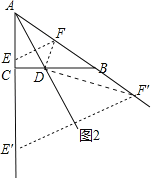
����ͼ2�У���BD��BFʱ��
��BD��4![]() ��
��
��BF��4![]() ��
��
��AE��AF��AB��BF��12��4![]() ��
��
����ͼ2�У���BF��BD=4![]() ʱ��
ʱ��
��AE��AF����AB+BF����12+4![]() ��
��
������������AE��ֵΪ0��12��4![]() ��12+4
��12+4![]() ʱ����BDF�ǵ��������Σ�
ʱ����BDF�ǵ��������Σ�
�ʴ�Ϊ����1��BC��4![]() ����2��y����
����2��y����![]() x+12
x+12![]() ��0��x��6������3����AE��ֵΪ0��12��4
��0��x��6������3����AE��ֵΪ0��12��4![]() ��12+4
��12+4![]() ʱ����BDF�ǵ��������Σ�
ʱ����BDF�ǵ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ÿ��С�����εı߳�����1�ķ���ֽ�У����߶�AB���߶�CD����A��B��C��D�Ķ˵㶼��С�����εĶ����ϣ�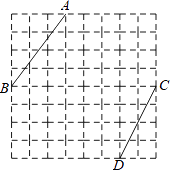
��1�����ڷ���ֽ�л���һ�����߶�ABΪһ�ߵ�����ABEF�����������εĸ����������С�����εĶ����ϣ����������Ϊ20��
���ڷ���ֽ����CDΪ�ױ�������������CDK����K��С�����εĶ����ϣ��ҡ�CDK�����Ϊ5��
��2���ڣ�1���������£�����BK����ֱ��д���߶�BK�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��x���������ϣ�����C������Ϊ��4��3����D��������y=��x2+6x��һ�㣬����x���Ϸ������BCD��������ֵΪ �� 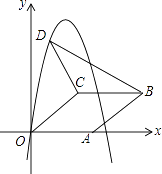
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��������ABC��AB����ƽ�Ƶõ�������DEF����֪AD��6��EF��8��CG��3������Ӱ���ֵ����Ϊ_____��
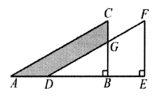
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��:
(1)��֪һ������![]() ,������ӡ���ĸͬʱ����1,������ֵ�������Ǽ�С?��˵���������.
,������ӡ���ĸͬʱ����1,������ֵ�������Ǽ�С?��˵���������.
(2)��������![]() �з��Ӻͷ�ĸͬʱ����2,3,��,k(����k>0),������?
�з��Ӻͷ�ĸͬʱ����2,3,��,k(����k>0),������?
(3)����������Ľ��۽������������:
����ѧ�涨:����סլ�����������С�ڵذ����,�����ɹ��,���������ذ�����ı�Ӧ��С��10%,���������ֵԽ��,סլ�IJɹ�����Խ��,��:ͬʱ������ȵĴ�������͵ذ����,סլ�IJɹ������DZ����,���DZ仵��?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��D��BA�ӳ����ϵ�һ�㣬��E��AC���е㡣
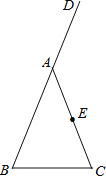
��1��ʵ������������ó߹水����Ҫ����ͼ������ͼ�б�����Ӧ��ĸ��������ͼ�ۼ�����д��������
������DAC��ƽ����AM��������BE���ӳ���AM�ڵ�F��
��2��������֤�����Բ���AF��BC��������λ�ù�ϵ��������ϵ����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��B=30�㣬BC=3����D��BC���ϵ�һ���㣨�����B��C�غϣ�������D��DE��BC��AB�ڵ�E������B��ֱ��DE���ۣ���B��������BC�ϵĵ�F��������AEFΪֱ��������ʱ��BD�ij�Ϊ �� 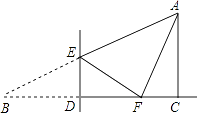
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�п쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ��������������ʻ��ʱ��Ϊx h������֮��ľ���Ϊy km����ͼ��ʾ�����߱�ʾy��x֮��ĺ�����ϵ������ͼ���������̽����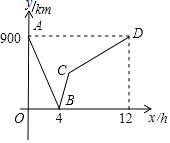
��1���ס�������֮��ľ���Ϊkm��
��2�������ͼ�е�B��ʵ�����壻
��3���������Ϳ쳵���ٶȣ�
��4�����߶�BC����ʾ��y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C��DΪ���ε��ĸ����㣬AB=16cm��BC=6cm������P��Q�ֱ�ӵ�A��Cͬʱ��������P��3cm/s���ٶ����B�ƶ�����Q��2cm/s���ٶ����D�ƶ�������P�˶�����Bֹͣʱ����QҲ��ֹ֮ͣ�˶���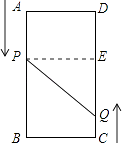
��1���ʼ����P�͵�Q�ľ�����10cm��
��2���ʼ������P��Q��D����Ϊ�����������Ϊֱ�������Σ�
����ʾ�����ݲ�ͬ���������ͬ��ͼ�Σ��ٸ��������⣮��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com