
【题目】如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为 . 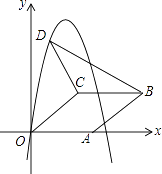
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的两条对角线AC,BD互相垂直,A1 , B1 , C1 , D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为 . 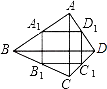
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
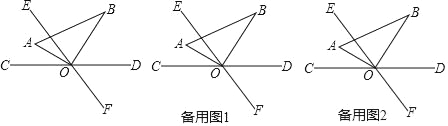
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列推理不正确的是( )
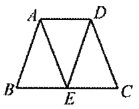
A.若∠AEB=∠C,则AE∥CD
B.若∠AEB=∠ADE,则AD∥BC
C.若∠C+∠ADC=180°,则AD∥BC
D.若∠AED=∠BAE,则AB∥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
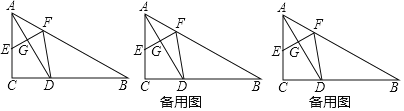
【题目】已知:如图,在△ABC中,∠C=90°,∠B=30°,AC=6,AD平分∠CAB交BC于D,E为射线AC上的一个动点,EF⊥AD交射线AB于点F,联结DF.
(1)求DB的长;
(2)当点E在线段AC上时,设AE=x,S△BDF=y,求y关于x的函数解析式;(S△BDF表示△BDF的面积)
(3)当AE为何值时,△BDF是等腰三角形.(请直接写出答案,不必写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com