
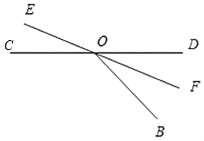
【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
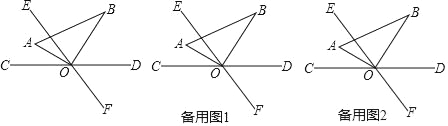
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
【答案】(1)∠BOD=60°;(2)当t=2.5s或32.5s时,直线EF平分∠AOB;②t的值为12s或36s.
【解析】
(1)依据∠COE=60°,OA平分∠COE,可得∠AOC=30°,再根据∠AOB=90°,即可得到∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况进行讨论:当OE平分∠AOB时,∠AOE=45°;当OF平分∠AOB时,AOF=45°;分别依据角的和差关系进行计算即可得到t的值;
②分两种情况进行讨论:当OE平分∠BOD时,∠BOE=![]() ∠BOD;当OF平分∠BOD时,∠DOF=
∠BOD;当OF平分∠BOD时,∠DOF=![]() ∠BOD;分别依据角的和差关系进行计算即可得出t的值.
∠BOD;分别依据角的和差关系进行计算即可得出t的值.
(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
当OE平分∠AOB时,∠AOE=45°,
即9t+30°﹣3t=45°,
解得t=2.5;
当OF平分∠AOB时,AOF=45°,
即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
当OE平分∠BOD时,∠BOE=![]() ∠BOD,
∠BOD,
即9t﹣60°﹣3t=![]() (60°﹣3t),
(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=![]() ∠BOD,
∠BOD,
即3t﹣(9t﹣240°)=![]() (3t﹣60°),
(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
故答案为:(1)∠BOD=60°;(2)当t=2.5s或32.5s时,直线EF平分∠AOB;②t的值为12s或36s.


科目:初中数学 来源: 题型:
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 . 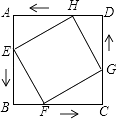
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.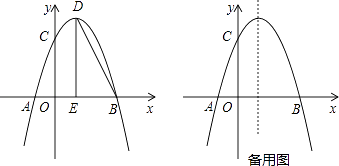
(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(Ⅲ)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
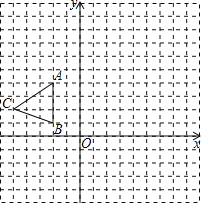
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)写出△A1B1C1的面积;△A2B2C2的面积.(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
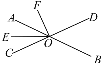
A. 95° B. 65°
C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为 . 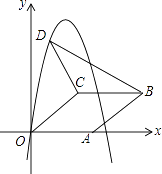
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y-2,则表示点A向右平移1个单位长度,再向下平移2个单位长度得到点A′.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A′(x-3,y),则线段AA′的长度是多少;
(2)已知点A(x,y),A′(x+2,y-1),则线段AA′的长度是多少;
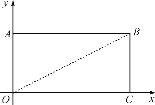
(3)长方形AOCB在平面直角坐标系中的位置如图所示,A(0,2),C(4,0),点A′(x′,y′),若x′=x+m,y′=y-2m(m均为正数),点A′(x′,y′)能否在△OCB的直角边上?若能,求m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探索:
(1)已知一个分数![]() ,如果分子、分母同时增加1,分数的值是增大还是减小?请说明你的理由.
,如果分子、分母同时增加1,分数的值是增大还是减小?请说明你的理由.
(2)若正分数![]() 中分子和分母同时增加2,3,…,k(整数k>0),情况如何?
中分子和分母同时增加2,3,…,k(整数k>0),情况如何?
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,问:同时增加相等的窗户面积和地板面积,住宅的采光条件是变好了,还是变坏了?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.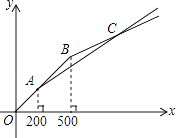
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com