
如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.

(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
(1)抛物线的解析式为y=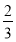 x2﹣4x﹣12;
x2﹣4x﹣12;
(2)①S=﹣(t﹣3)2+9,(0<t<6),
②当t=3时,S取最大值为9,点R坐标为(3,﹣18),理由见解析.
【解析】
试题分析:(1)把点A代入解析式求出c和a,最后根据抛物线的对称轴求出b,即可求出最后结果.
(2)①本题需根据题意列出S与t的关系式,再整理即可求出结果.
②本题需分三种情况:当点R在BQ的左边,且在PB下方时;当点R在BQ的左边,且在PB上方时;当点R在BQ的右边,且在PB上方时,然后分别代入抛物线的解析式中,即可求出结果.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c,
由题意知点A(0,﹣12),
所以c=﹣12,
又18a+c=0,
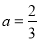 ,
,
∵AB∥OC,且AB=6,
∴抛物线的对称轴是x=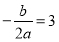 ,
,
∴b=﹣4,
所以抛物线的解析式为y=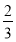 x2﹣4x﹣12;
x2﹣4x﹣12;
(2)①S= ·2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,(0<t<6),
·2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,(0<t<6),
②当t=3时,S取最大值为9.
这时点P的坐标(3,﹣12),
点Q坐标(6,﹣6),
若以P、B、Q、R为顶点的四边形是平行四边形,有如下三种情况:
(Ⅰ)当点R在BQ的左边,且在PB下方时,点R的坐标(3,﹣18),将(3,﹣18)代入抛物线的解析式中,满足解析式,所以存在,点R的坐标就是(3,﹣18),
(Ⅱ)当点R在BQ的左边,且在PB上方时,点R的坐标(3,﹣6),将(3,﹣6)代入抛物线的解析式中,不满足解析式,所以点R不满足条件.
(Ⅲ)当点R在BQ的右边,且在PB上方时,点R的坐标(9,﹣6),将(9,﹣6)代入抛物线的解析式中,不满足解析式,所以点R不满足条件.
综上所述,点R坐标为(3,﹣18).
考点:二次函数综合题.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:填空题
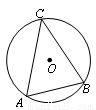
如图,⊙O的半径为4,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:选择题
若a与3互为倒数,则a等于( )
A.3 B.-3 C. D.-
D.-
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球( )
A.12个 B.16个 C.20个 D.30个
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:解答题
“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:

⑴这次共抽查了 个家长;
⑵请补全条形统计图和扇形统计图(友情提醒:条形图补画家长持“反对”态度的人数条,扇形图填上“反对”及“赞成”的百分数);
⑶已知该校共有1200名学生,持“赞成”态度的学生估计约有 人.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:填空题
已知圆锥的底面半径是3cm,母线长为6cm,则这个圆锥的侧面积为____ ___cm2.(结果保留π)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:解答题
已知直线 与x轴、y轴分别交于B点、A点,直线
与x轴、y轴分别交于B点、A点,直线 与x轴、y轴分别交于D点、E点,两条直线交于点C,求⊿BCD的外接圆直径的长度。
与x轴、y轴分别交于D点、E点,两条直线交于点C,求⊿BCD的外接圆直径的长度。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com