【题目】如图，以O为圆心的两个同心圆，大圆半径为5，小圆半径为，点P为大圆上的一点，PC、PB切小圆于点A、点B，交大圆于C、D两点，点E为弦CD上任一点，则AE+OE的最小值为 .

参考答案：

【答案】

【解析】

试题分析：连接PO，并延长OP到O′交CD于点G，使OG=O′G，连接AO′交CD于点E，连接OE，过点A作AF⊥OP，垂足为F，由切线的性质可知OB⊥PD，由垂径定理可知PB=BD，在Rt△OPB中，由勾股定理可知PB=2，故此PD=4，同理可知PC=4，从而得到PC=PD，然后证明PO平分∠CPD，由等腰三角形三线合一的性质可知PG⊥DC，依据锐角三角函数的定义可知OF=1，AF=2，PG=8，从而求得OO′=7，在Rt△AFO′中，由勾股定理可知AO′=.

解：如图所示：连接PO，并延长OP到O′交CD于点G，使OG=O′G，连接AO′交CD于点E，连接OE，过点A作AF⊥OP，垂足为F.

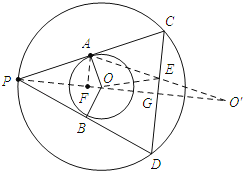
∵PB是小圆的切线，

∴OB⊥PD.

∴PB=BD.

在Rt△OPB中，PB===2.

∴PD=4.

同理：PC=4.

∴PC=PD.

∵PA、PB是小圆的切线，

∴PO平分∠CPD.

∴PG⊥DC.

∴CD是OO′的垂直平分线.

∴OE=O′E.

∴AE+EO=AE+EO′=AO′.

∵cos∠AOF==，

∴OF=AO×cos∠AOF==1，AF=2OF=2.

∵PG=PC×==8，

∴OG=PG﹣OP=3.

∴OO′=1+3+3=7.

在Rt△AFO′中，AO′===.

故答案为：.

关闭